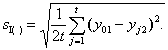ГОСТ Р ИСО 5725-3-2002

ТОЧНОСТЬ
(ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ)
МЕТОДОВ И РЕЗУЛЬТАТОВ
ИЗМЕРЕНИЙ

Часть 3

Промежуточные показатели прецизионности
стандартного метода измерений

ГОССТАНДАРТ РОССИИ

Москва

Предисловие

1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологической службы» Госстандарта России (ВНИИМС), Всероссийским научно-исследовательским институтом стандартизации (ВНИИСтандарт), Всероссийским научно-исследовательским институтом классификации, терминологии и информации по стандартизации и качеству (ВНИИКИ) Госстандарта России

ВНЕСЕН Управлением метрологии и Научно-техническим управлением Госстандарта России

2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 23 апреля 2002 г. № 161-ст

3 Настоящий стандарт представляет собой полный аутентичный текст международного стандарта ИСО 5725-3:1994 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений»

4 ВВЕДЕН ВПЕРВЫЕ

СОДЕРЖАНИЕ

ПРЕДИСЛОВИЕ К ГОСУДАРСТВЕННЫМ СТАНДАРТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002 ПОД ОБЩИМ ЗАГОЛОВКОМ «ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ»

Целью разработки Государственных стандартов Российской Федерации ГОСТ Р ИСО 5725-1-2002, ГОСТ Р ИСО 5725-2-2002, ГОСТ Р ИСО 5725-3-2002, ГОСТ Р ИСО 5725-4-2002, ГОСТ Р ИСО 5725-5-2002, ГОСТ Р ИСО 5725-6-2002, далее - ГОСТ Р ИСО 5725, является прямое применение в Российской Федерации шести частей основополагающего международного стандарта ИСО 5725 под общим заголовком «Точность (правильность и прецизионность) методов и результатов измерений» в практической деятельности по метрологии (разработке, аттестации и применению методик выполнения измерений), стандартизации методов контроля (испытаний, измерений, анализа), испытаниям продукции, в том числе для целей подтверждения соответствия, оценке компетентности испытательных лабораторий согласно требованиям ГОСТ Р ИСО/МЭК 17025-2000.

ГОСТ Р ИСО 5725 представляют собой полный аутентичный текст шести частей международного стандарта ИСО 5725, в том числе:

ГОСТ Р ИСО 5725-1-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения»;

ГОСТ Р ИСО 5725-2-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений»;

ГОСТ Р ИСО 5725-3-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений»;

ГОСТ Р ИСО 5725-4-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений»;

ГОСТ Р ИСО 5725-5-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений»;

ГОСТ Р ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике».

Каждая часть содержит аутентичный перевод предисловия и введения к международному стандарту ИСО 5725, а также предисловие к государственным стандартам Российской Федерации (ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002) и издается самостоятельно.

Пользование частями 2 - 6 ГОСТ Р ИСО 5725 в отдельности возможно только совместно с частью 1 (ГОСТ Р ИСО 5725-1), в которой установлены основные положения и определения, касающиеся всех частей ГОСТ Р ИСО 5725.

В соответствии с основными положениями ИСО 5725-1 (пункт 1.2) настоящий стандарт распространяется на методы измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающие в качестве результата измерений единственное значение. При этом это единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.

Стандарты ИСО 5725 могут применяться для оценки точности выполнения измерений различных физических величин, характеризующих измеряемые свойства того или иного объекта, в соответствии со стандартизованной процедурой. При этом в пункте 1.2 ИСО 5725-1 особо отмечено, что стандарт может применяться для оценки точности выполнения измерений состава и свойств очень широкой номенклатуры материалов, включая жидкости, порошкообразные и твердые материалы - продукты материального производства или существующие в природе, при условии, что учитывают любую неоднородность материала.

Применяемый в международных стандартах термин «стандартный метод измерений» адекватен отечественному термину «стандартизованный метод измерений».

В ИСО 5725:1994 - 1998 и ИСО/МЭК 17025-99 понятие «метод измерений» («measurement method») включает совокупность операций и правил, выполнение которых обеспечивает получение результатов с известной точностью. Таким образом, понятие «метод измерений» по ИСО 5725 и ИСО/МЭК 17025 адекватно понятию «методика выполнения измерений (МВИ)» по ГОСТ Р 8.563-96 «Государственная система обеспечения единства измерений. Методики выполнения измерений» (пункт 3.1) и соответственно значительно шире по смыслу, чем определение термина «метод измерений» в Рекомендации по межгосударственной стандартизации РМГ 29-99 «Государственная система обеспечения единства измерений. Метрология. Основные термины и определения» (пункт 7.2).

Более того, в оригинале ИСО 5725 очень часто употребляется в качестве понятия «метод измерений» и английский термин «test method», перевод которого на русский язык - «метод испытаний» (см. примечание 1 к пункту 3.2 ИСО 5725-1) и который по смыслу совпадает с термином 6.2 ИСО 5725-1 «standard measurement method» (стандартизованный метод измерений). Соответственно в качестве термина «результат измерений» в оригинале стандарта чаще используется английский термин «test result» (см. пункт 3.2 ИСО 5725-1), причем в контексте как с термином «test method» (см. пункт 3.2), так и с термином «measurement method» (см. в оригинале, например, пункты 1.2 или 7.2.1 ИСО 5725-1).

При этом следует иметь в виду, что область применения ИСО 5725 - точность стандартизованных методов измерений, в том числе предназначенных для целей испытаний продукции, позволяющих количественно оценить характеристики свойств (показателей качества и безопасности) объекта испытаний (продукции). Именно поэтому во всех частях стандарта результаты измерений характеристик образцов, взятых в качестве выборки из партии изделий (или проб, отобранных из партии материала), являются основой для получения результатов испытаний всей партии (объекта испытаний). Когда объектом испытаний является конкретный образец (test speciment, sample), результаты измерений и испытаний могут совпадать. Такой подход имеет место в примерах по определению показателей точности стандартного (стандартизованного) метода измерений, содержащихся в ИСО 5725.

Следует отметить, что в отечественной метрологии точность (accuracy) и погрешность (error) результатов измерений, как правило, определяются сравнением результата измерений с истинным или действительным (условно истинным) значением измеряемой физической величины (являющимися фактически эталонными значениями измеряемых величин, выраженными в узаконенных единицах).

В условиях отсутствия необходимых эталонов, обеспечивающих воспроизведение, хранение и передачу соответствующих значений единиц величин, необходимых для оценки погрешности (точности) результатов измерений, и в отечественной, и в международной практике за действительное значение зачастую принимают общее среднее значение (математическое ожидание) установленной (заданной) совокупности результатов измерений. В ИСО 5725 эта ситуация отражена в термине «принятое опорное значение» (см. пункты 3.5 и 3.6 ГОСТ Р ИСО 5725-1) и рекомендуется ГОСТ Р ИСО 5725-1 для использования в этих случаях и в отечественной практике.

Термины «правильность» (trueness) и «прецизионность» (precision) в отечественных нормативных документах по метрологии до настоящего времени не использовались. При этом «правильность» - степень близости результата измерений к истинному или условно истинному (действительному) значению измеряемой величины или в случае отсутствия эталона измеряемой величины - степень близости среднего значения, полученного на основании большой серии результатов измерений (или результатов испытаний) к принятому опорному значению. Показателем правильности обычно является значение систематической погрешности (см. пункт 3.7 ГОСТ Р ИСО 5725-1).

В свою очередь «прецизионность» - степень близости друг к другу независимых результатов измерений, полученных в конкретных установленных условиях. Эта характеристика зависит только от случайных факторов и не связана с истинным или условно истинным значением измеряемой величины (см. пункт 3.12 ГОСТ Р ИСО 5725-1). Мера прецизионности обычно вычисляется как стандартное (среднеквадратическое) отклонение результатов измерений, выполненных в определенных условиях. Количественные значения мер прецизионности существенно зависят от заданных условий. Экстремальные показатели прецизионности - повторяемость, сходимость (repeatability) и воспроизводимость (reproducibility) регламентируют и в отечественных нормативных документах, в том числе в большинстве государственных стандартов на методы контроля (испытаний, измерений, анализа) (см. пункты 3.12 - 3.20 ГОСТ Р ИСО 5725-1).

В соответствии с ИСО 5725 цель государственных стандартов ГОСТ Р ИСО 5725 состоит в том, чтобы:

а) изложить основные положения, которые следует иметь в виду при оценке точности (правильности и прецизионности) методов и результатов измерений при их применении, а также при планировании экспериментов по оценке различных показателей точности (ГОСТ Р ИСО 5725-1);

б) регламентировать основной способ экспериментальной оценки повторяемости (сходимости) и воспроизводимости методов и результатов измерений (ГОСТ Р ИСО 5725-2);

в) регламентировать процедуру получения промежуточных показателей прецизионности методов и результатов измерений, изложив условия их применения и методы оценки (ГОСТ Р ИСО 5725-3);

г) регламентировать основные способы определения правильности методов и результатов измерений (ГОСТ Р ИСО 5725-4);

д) регламентировать для применения в определенных обстоятельствах несколько альтернатив основным способам (ГОСТ Р ИСО 5725-2 и ГОСТ Р ИСО 5725-4) определения прецизионности и правильности методов и результатов измерений, приведенных в ГОСТ Р ИСО 5725-5;

е) изложить некоторые практические применения показателей правильности и прецизионности (ГОСТ Р ИСО 5725-6).

Представленные в виде таблицы рекомендации по применению основных положений ГОСТ Р ИСО 5725 в деятельности по метрологии, стандартизации, испытаниям, оценке компетентности испытательных лабораторий со ссылками на нормы государственных стандартов Российской Федерации, содержащих требования к выполнению соответствующих работ, приведены в приложении к предисловию в ГОСТ Р ИСО 5725-1.

Алгоритмы проведения экспериментов по оценке повторяемости, воспроизводимости, промежуточных показателей прецизионности, показателей правильности (характеристик систематической погрешности) методов и результатов измерений рекомендуется внедрять через программы экспериментальных метрологических исследований показателей точности (характеристик погрешности) результатов измерений, выполняемых по разрабатываемой МВИ, и (или) через программы контроля показателей точности применяемых МВИ.

Использование приведенных в приложениях А к каждому стандарту условных обозначений в качестве обязательных рекомендуется только для тех показателей точности, которые до настоящего времени в отечественной метрологической практике не использовались (например, для показателей по пунктам 3.9 - 3.12 ГОСТ Р ИСО 5725-1). Для остальных показателей и критериев используемые в ГОСТ Р ИСО 5725 условные обозначения, как правило, могут применяться наряду с условными обозначениями этих показателей и критериев, принятых в действующих отечественных документах (например, предел повторяемости (сходимости) с условным обозначением r по пункту 3.16 ГОСТ Р ИСО 5725-1 наряду с условным обозначением d, принятым для этого показателя в ряде рекомендаций по метрологии, а также в государственных стандартах на методы испытаний продукции).

ПРЕДИСЛОВИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725

Международная организация по стандартизации (ИСО) является Всемирной федерацией национальных организаций по стандартизации (комитетов - членов ИСО). Разработка международных стандартов обычно осуществляется техническими комитетами ИСО. Каждый член ИСО, заинтересованный в деятельности соответствующего технического комитета, имеет право быть представленным в этом комитете. Правительственные и неправительственные международные организации, сотрудничающие с ИСО, также принимают участие в этой работе. ИСО тесно сотрудничает с Международной электротехнической комиссией (МЭК) по всем вопросам стандартизации в области электротехники.

Проекты международных стандартов, принятые техническими комитетами, направляются техническим комитетам - членам ИСО на голосование перед их утверждением Советом ИСО в качестве международных стандартов. Стандарты утверждаются в качестве международных в соответствии с установленными в ИСО требованиями: в случае их одобрения по меньшей мере 75 % комитетов - членов ИСО, принимавших участие в голосовании.

Международный стандарт ИСО 5725-3 был подготовлен Техническим комитетом ИСО/ТК 69 «Применение статистических методов», Подкомитетом ПК 6 «Методы и результаты измерений».

ИСО 5725 состоит из следующих частей под общим заголовком «Точность (правильность и прецизионность) методов и результатов измерений»:

Часть 1. Основные положения и определения

Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений

Часть 3. Промежуточные показатели прецизионности стандартного метода измерений

Часть 4. Основные методы определения правильности стандартного метода измерений

Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений

Часть 6. Использование значений точности на практике

ИСО 5725 (части 1 - 6) в совокупности аннулирует и заменяет ИСО 5725:1986, область распространения которого была расширена включением правильности (в дополнение к прецизионности) и условий промежуточной прецизионности (в дополнение к условиям повторяемости и воспроизводимости).

Приложения A, B и C являются обязательными для настоящей части ИСО 5725, приложения D и E - справочные.

ВВЕДЕНИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725

0.1 В ИСО 5725 для описания точности метода измерений используют два термина: «правильность» и «прецизионность». Термин «правильность» характеризует степень близости среднего значения большого числа результатов испытаний к истинному или принятому опорному значению, термин «прецизионность» характеризует степень близости результатов испытаний друг к другу.

0.2 Общие положения об этих понятиях представлены в ИСО 5725-1 и поэтому здесь не повторяются. Эта часть ИСО 5725 должна применяться совместно с ИСО 5725-1, поскольку в ней даны определения и общие положения.

0.3 На изменчивость результатов измерений, выполненных по одному методу, помимо различий между предположительно идентичными образцами могут влиять многие различные факторы, в том числе:

a) оператор;

b) используемое оборудование;

c) калибровка оборудования;

d) параметры окружающей среды (температура, влажность, загрязнение воздуха и т.д.);

e) партии реактивов;

f) время между измерениями.

Различия между результатами измерений, выполняемых разными операторами и/или с использованием различного оборудования, как правило, будут больше, чем между результатами измерений, выполняемых в течение короткого интервала времени одним оператором с использованием одного и того же оборудования.

0.4 Для описания изменчивости метода измерений необходимо и во многих практических случаях полезно использовать два условия прецизионности, названные условиями повторяемости и воспроизводимости. В условиях повторяемости факторы а) - е) в 0.3 считают постоянными и они не влияют на изменчивость, в то время как в условиях воспроизводимости они непостоянны и способствуют изменчивости результатов измерений. Таким образом, условия повторяемости и воспроизводимости являются двумя экстремальными условиями прецизионности, причем первым соответствует минимальная, а вторым - максимальная изменчивость результатов. Промежуточные условия между этими двумя экстремальными условиями прецизионности соответствуют случаям, когда один или большее число факторов а) - f) могут меняться и применяются в определенных регламентированных условиях выполнения измерений.

Прецизионность, как правило, выражают через стандартные отклонения.

0.5 В настоящей части ИСО 5725 основное внимание сосредоточено на промежуточных показателях прецизионности метода измерений. Такие показатели называют промежуточными по той причине, что их численные значения располагаются между двумя экстремальными показателями прецизионности метода измерений: значениями стандартных отклонений повторяемости и воспроизводимости.

Иллюстрацией необходимости в такого рода промежуточных показателях прецизионности является работа современной лаборатории, обслуживающей производственное предприятие с трехсменным режимом работы, где измерения осуществляются разными операторами на различном оборудовании. Операторы и оборудование в этом случае - факторы, способствующие изменчивости результатов измерений, и их необходимо принимать во внимание при оценке прецизионности метода измерений.

0.6 Промежуточные показатели прецизионности, определяемые в настоящей части ИСО 5725, используют прежде всего, в случаях, когда их оценка является частью программы (процедуры), разработки, стандартизации или внутрилабораторного контроля точности метода измерений. Эти показатели также могут оцениваться в специально спланированном межлабораторном эксперименте, однако их интерпретация и применение в таком случае требуют осмотрительности по причинам, разъясненным в 1.3 и 9.1.

0.7 Основные факторы, которые с наибольшей вероятностью могут оказывать влияние на прецизионность метода измерений:

a) время - является ли интервал времени между следующими одно за другим измерениями коротким или длительным?;

b) калибровка - подвергается ли или нет одно и то же оборудование перекалибровке между следующими одна за другой группами измерений?;

c) оператор - выполняет ли следующие одно за другим измерения один и тот же оператор или разные операторы?;

d) оборудование - используется ли при измерениях одно и то же или различное оборудование (либо реактивы из одних и тех же партий, либо из разных партий)?

0.8 Чтобы учесть изменения условий выполнения измерений (время, калибровка, оператор и оборудование) в пределах лаборатории, полезно ввести следующие промежуточные условия прецизионности с числом изменяющихся факторов M (M = 1, 2, 3 или 4):

a) только один из четырех факторов изменяется (M = 1);

b) два из четырех факторов изменяются (M = 2);

c) три из четырех факторов изменяются (M = 3);

d) все четыре фактора изменяются (M = 4).

Различные промежуточные условия прецизионности являются причиной различных значений стандартных отклонений прецизионности (промежуточных стандартных отклонений), обозначаемых s_{I( )}, где в скобках приводят конкретные условия. Например, s_I(TO) представляет собой стандартное отклонение промежуточной прецизионности при выполнении измерений в разные интервалы времени (T) и разными операторами (O).

0.9 Промежуточные условия прецизионности имеют место, когда изменяется один или более факторов, перечисленных в 0.7. В условиях повторяемости предполагается, что данные факторы являются неизменными.

Стандартное отклонение результатов измерений, полученных в условиях повторяемости, как правило, меньше, чем в случае, когда результаты получены в промежуточных условиях прецизионности. Обычно при химическом анализе стандартное отклонение в промежуточных условиях прецизионности может быть в два или три раза больше, чем стандартное отклонение в условиях повторяемости. Разумеется, оно не должно выходить за пределы стандартного отклонения воспроизводимости.

В качестве примера при определении меди в медной руде совместный эксперимент, охватывавший 35 лабораторий, показал, что стандартное отклонение в промежуточных условиях прецизионности с одним изменяющимся фактором (оператор и оборудование те же самые, но интервалы времени проведения измерения различные) оказалось в 1,5 раза больше, чем в условиях повторяемости как для метода электролитической гравиметрии, так и для метода титрования Na₂S₂O₃.

ГОСТ Р ИСО 5725-3-2002

ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Часть 3

Промежуточные показатели прецизионности стандартного метода измерений

Accuracy (trueness and precision) of measurement methods and results.
Part 3. Intermediate measures of the precision of a standard measurement method

1 Область применения

1.1 Настоящий стандарт устанавливает четыре промежуточных показателя прецизионности, обусловленных изменениями условий эксперимента (время, калибровка, оператор и оборудование) в пределах лаборатории. Показатели могут быть установлены посредством эксперимента в пределах определенной лаборатории или путем межлабораторного эксперимента.

Кроме того, в настоящем стандарте:

a) рассматривают сущность определений промежуточных показателей прецизионности;

b) представлено руководство по интерпретации и применению оценок промежуточных показателей прецизионности на практике;

c) не рассматриваются вопросы, связанные с ошибками при оценке промежуточных показателей прецизионности;

d) не рассматриваются вопросы оценки правильности самого метода измерений, однако рассматриваются связи между правильностью и условиями измерений.

1.2 Настоящий стандарт относится исключительно к методам измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающим в качестве результата измерений единственное значение. При этом это единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.

1.3 Суть определения промежуточных показателей прецизионности заключается в том, чтобы на их основе оценить способность метода измерений к повторению результатов измерений в точно определенных условиях.

1.4 Статистические методы, излагаемые в настоящем стандарте, основываются на предпосылке, заключающейся в том, что можно свести воедино информацию по «похожим» условиям выполнения измерений с целью получения более точной и надежной информации по промежуточным показателям прецизионности. Эта предпосылка верна при условии, что объявляемое «похожим» в действительности является таковым. Однако довольно трудно придерживаться данной предпосылки в случае оценки промежуточных показателей прецизионности на основе межлабораторного эксперимента. При этом, например, бывает трудно определить, являются ли «похожими» для различных лабораторий факторы «времени» или «оператора», так чтобы группируемая от лабораторий информация имела смысл. Следовательно, использование результатов межлабораторного эксперимента для оценки промежуточных показателей прецизионности требует осмотрительности. Внутрилабораторные исследования также опираются на данную предпосылку, однако она обычно бывает более реалистичной, так как контроль и знание фактического влияния фактора в этом случае в большей степени находятся в пределах досягаемости аналитика.

1.5 Для оценки и подтверждения промежуточных показателей прецизионности в пределах лаборатории, помимо описанных в настоящем стандарте, существуют и другие методы, например метод контрольных карт (см. ГОСТ Р ИСО 5725-6). Настоящий стандарт не претендует на описание единственно возможного подхода к оценке промежуточных показателей прецизионности в пределах конкретной лаборатории.

Примечание 1 - В настоящем стандарте используют понятие вложенных экспериментов различных типов. Основная информация по этому поводу представлена в приложениях B и C.

2 Нормативные ссылки

В настоящем стандарте использованы ссылки на следующие стандарты:

ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения

ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений

ГОСТ Р ИСО 5725-4-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений

ГОСТ Р ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике

3 Определения

В настоящем стандарте используют определения, приведенные в ГОСТ Р ИСО 5725-1 и ИСО 3534-1 [1].

Условные обозначения, используемые в ГОСТ Р ИСО 5725, даны в приложении А.

4 Общее требование

Чтобы измерения осуществлялись по одной и той же процедуре, метод измерений должен быть стандартизован. Все измерения, являющиеся частью внутрилабораторного или межлабораторного эксперимента, должны выполняться в соответствии с таким стандартом.

5 Основные факторы

5.1 В условиях выполнения измерений в пределах лаборатории основной вклад в изменчивость измерений вносят четыре фактора: время, калибровка, оператор и оборудование (см. таблицу 1).

5.2 Выражение «измерения, выполняемые в одно и то же время» подразумевают измерения, которые проводят за столь короткий, насколько это возможно, период времени, чтобы свести к минимуму изменения в условиях выполнения измерений, таких как условия окружающей среды, неизменность которых нельзя гарантировать всегда. Выражение «измерения, выполняемые в разное время» подразумевает измерения, выполняемые в течение длительных интервалов времени, которые могут быть подвержены влияниям изменений окружающей среды.

Таблица 1 - Основные факторы и их состояния

5.3 Термин «калибровка» не подразумевает здесь какой-либо калибровки, являющейся неотъемлемой частью процедуры получения результата измерений при реализации данного метода измерений. Он относится к процессу калибровки, выполняемому в лаборатории периодически, через регулярные промежутки между выполнением групп измерений.

5.4 В некоторых процедурах термин «оператор» может представлять собой в действительности группу операторов, каждый из которых выполняет какую-либо определенную часть процедуры. В таком случае группа должна рассматриваться как один оператор, и любое изменение в составе или распределении обязанностей внутри группы должно рассматриваться как фактор смены оператора.

5.5 Термин «оборудование» часто представляет собой комплекты оборудования, и любое изменение в каком бы то ни было существенном компоненте комплекта должно рассматриваться как фактор «разное оборудование». Что касается того, что считать «существенным компонентом», то здесь должен превалировать здравый смысл. Например, смену термометра при измерениях температуры следовало бы считать существенным компонентом, а использование же слегка отличающегося сосуда для водяной бани можно считать не заслуживающим внимания. Смену партии реактива (при выполнении физико-химических измерений) следует рассматривать существенным компонентом. Это может соответствовать различному «оборудованию» или перекалибровке, если после такой смены следует калибровка.

5.6 В условиях повторяемости все четыре фактора соответствуют состоянию 1 таблицы 1. Для промежуточных условий прецизионности один или больше факторов соответствуют состоянию 2 таблицы 1 и определяются как «условия прецизионности с числом изменяющихся факторов M», где M - количество факторов в состоянии 2. В условиях воспроизводимости результаты получают в разных лабораториях, так что не только все четыре фактора соответствуют состоянию 2, но помимо этого имеют место дополнительные влияющие факторы вследствие различий между лабораториями в организации работы, в техническом состоянии, в общем уровне квалификации операторов, в стабильности и проверке результатов измерений и т.д.

5.7 В промежуточных условиях прецизионности с M изменяющимися факторами необходимо конкретизировать с помощью подстрочных индексов, какие факторы соответствуют состоянию 2 таблицы 1, например:

- стандартное отклонение промежуточной прецизионности (при различиях по фактору «время») - s_I(T);

- стандартное отклонение промежуточной прецизионности (при различиях по фактору «калибровка») - s_I(C);

- стандартное отклонение промежуточной прецизионности (при различиях по фактору «оператор») - s_I(O);

- стандартное отклонение промежуточной прецизионности (при различиях по факторам «время» и «оператор») - s_I(TO);

- стандартное отклонение промежуточной прецизионности (при различиях по факторам «время», «оператор» и «оборудование») - s_I(TOE);

- многие другие факторы конкретизируют аналогичным образом.

6 Статистическая модель

6.1 Базовая модель

Для оценки точности (правильности и прецизионности) метода измерений каждый результат измерений полезно представить в виде суммы трех составляющих:

y = m + B + e,                                                             (1)

где для определенного испытуемого материала:

m - общее среднее значение (математическое ожидание);

B - лабораторная составляющая систематической погрешности конкретной методики выполнения измерений в условиях повторяемости в пределах лаборатории;

e - случайная погрешность результата каждого измерения в условиях повторяемости.

Далее рассматривают каждую из этих составляющих и детали этой базовой модели.

6.2 Общее среднее значение m

6.2.1 Общее среднее значение m представляет собой среднее значение по совокупности результатов измерений. Значение m, получаемое при совместном исследовании (см. ГОСТ Р ИСО 5725-2), зависит исключительно от «истинного значения» и метода измерений и не зависит от лаборатории, оборудования, оператора или времени, при которых был получен любой результат измерений. Общее среднее значение измеряемой характеристики определенного материала называют «уровнем испытаний»; в частности, образцы различной продукции или других материалов с различной степенью чистоты (например, марки стали) будут соответствовать различным уровням.

Во многих ситуациях оправдано введение понятия истинного значения μ, например, если μ - истинная концентрация раствора, который титруют. Уровень m, как правило, не равен истинному значению; разность (m - μ) называется систематической погрешностью метода измерений (методики выполнения измерений).

В некоторых случаях уровень испытаний определяется исключительно методом измерений, и понятие независимого истинного значения измеряемой величины не применяется; например, к такой категории испытуемых характеристик относят такие условные величины, как твердость стали по Виккерсу и Микум-индексы кокса. Однако в общем случае систематическую погрешность обозначают δ (δ = 0, где не существует истинного значения измеряемой величины), тогда общее среднее значение т составляет

m = μ + δ.                                                                        (2)

Примечание 2 - Рассмотрение термина «систематическая погрешность δ» представлено в ГОСТ Р ИСО 5725-1; описание экспериментов по оценке правильности представлено в ГОСТ Р ИСО 5725-4.

6.2.2 Систематическая погрешность метода измерений может не оказывать никакого влияния на расхождения между результатами измерений, полученными данным методом, и ею можно пренебречь, если только она не зависит от значения измеряемой характеристики (уровня испытаний). Однако систематическая погрешность метода измерений должна учитываться при сопоставлении результатов измерений со значением измеряемой характеристики, установленным в контракте, или со стандартизованным значением в случае, когда в контракте или технических условиях упоминается истинное значение μ, а не уровень испытаний m, либо при сопоставлении результатов измерений, полученных с использованием различных методов измерений.

6.3 Составляющая B

6.3.1 Составляющая B является слагаемым, представляющим отклонение результата лаборатории от m по какой-либо одной или большему числу причин, независимо от случайной погрешности e, имеющей место в каждом результате измерений. В условиях повторяемости в одной лаборатории для конкретного метода измерений B считают неизменным и называют «лабораторной составляющей систематической погрешности конкретного метода измерений (МВИ)».

6.3.2 При регулярном использовании метода измерений становится очевидным, что предельное значение B представляет большое число составляющих, обусловленных различными влияющими факторами, например, сменами оператора, применяемого оборудования, калибровкой оборудования и изменениями условий окружающей среды (температуры, влажности, загрязнения атмосферного воздуха и т.д.). Статистическая модель [равенство (1)] в таком случае может быть переписана в виде

y = m + B₀ + B₍₁₎ + B₍₂₎ + ,…, + e                                          (3)

или

y = μ + δ + B₀ + B₍₁₎ + B₍₂₎ +,..., + e,                                        (4)

где B формируется из вкладов изменяющихся факторов B₀, B₍₁₎, B₍₂₎ и может включать в себя факторы промежуточных условий прецизионности.

На практике пределы использования описанной модели будут определяться возможностями исследования и оценки чувствительности метода измерений. Во многих случаях достаточными будут сокращенные формы модели.

6.4 Слагаемые B₀ + B₍₁₎ + B₍₂₎ и т.д.

6.4.1 В условиях повторяемости все эти слагаемые остаются неизменными и их суммируют с систематической погрешностью результатов измерений. В промежуточных условиях прецизионности B₀ представляет собой определенную величину, вызванную влияющими факторами, остающимися без изменения (состояние 1 в таблице 1), в то время как B₍₁₎, B₍₂₎ и т.д. представляют собой случайные величины, вызванные изменениями влияющих факторов (состояние 2 в таблице 1). Они больше не являются составляющими систематической погрешности, однако увеличивают значение стандартного отклонения промежуточной прецизионности таким образом, что оно становится больше стандартного отклонения повторяемости.

6.4.2 Влияющие эффекты, обусловленные различиями между операторами, отображают персональные навыки при выполнении измерений (например, в считывании показаний шкалы и т.д.). Некоторые из этих различий можно устранить или уменьшить стандартизацией метода измерений, в частности, четкими и точными описаниями предусматриваемых технологических приемов (выполняемых процедур). Несмотря на это, какая-то систематическая погрешность в результатах измерений, полученных одним оператором, всегда остается, причем она не всегда является постоянной (например, абсолютная величина систематической погрешности будет меняться в зависимости от психического и/или физического состояния оператора в этот день). Такая систематическая погрешность не может быть скорректирована или устранена точной калибровкой. Ее абсолютную величину необходимо снижать путем использования четкой инструкции по выполнению измерений и совершенствования квалификации оператора. В этих условиях эффект смены операторов может рассматриваться как носящий случайный характер.

6.4.3 Влияющие эффекты, вызванные применением разного оборудования, обусловлены различиями в местах установки оборудования, особенно флуктуациями показаний и т.д. Некоторые из таких эффектов могут быть скорректированы точной калибровкой. Расхождения, обусловленные различиями систематического характера в оборудовании, также следует исправлять путем калибровки, и такого рода процедура должна быть предусмотрена в стандартном методе. Например, смена партий реактива может быть нивелирована также путем калибровки оборудования с использованием соответствующего стандартного образца, который должен выбираться в соответствии с рекомендациями Руководства ИСО 33* [2] и Руководства ИСО 35* [3]. Остаточную погрешность оборудования, которое было калибровано с применением стандартного образца, рассматривают как случайную.

6.4.4 Влияющие эффекты, обусловленные временем, могут быть вызваны различиями в условиях окружающей среды, такими как изменения комнатной температуры, влажности и т.д. Стандартизация условий окружающей среды сводит к минимуму влияние данных эффектов.

6.4.5 Влияние квалификации или усталости оператора может рассматриваться как взаимодействие факторов оператора и времени. Функционирование комплекта оборудования может быть различным в начале и после его использования в течение многих часов: это пример взаимодействия факторов оборудования и времени. Когда численность операторов невелика, а количество комплектов оборудования еще меньше, эффекты, являющиеся следствием данных факторов, могут быть оценены как фиксированные (не случайные).

6.4.6 Процедуры, представленные в ГОСТ Р ИСО 5725-2, разработаны с учетом допущения, что распределение лабораторных составляющих систематической погрешности является приближенно нормальным, но на практике они (процедуры) используют для большинства распределений других типов при условии, что данные распределения являются унимодальными. Дисперсия B носит название межлабораторной дисперсии и выражается в виде:

var(B) = σ_L².                                                            (5)

Дисперсия будет также включать эффекты от изменений, обусловленных оператором, оборудованием, временем и окружающей средой. Дисперсии промежуточной прецизионности можно рассчитать на основе данных эксперимента вложенного типа по оценке прецизионности с использованием разных операторов, разного времени измерений, разных условий окружающей среды и т.д. При этом var(B) рассматривают как величину, состоящую из независимых составляющих, представляющих лабораторию, оператора, день эксперимента, условия окружающей среды и т.д.

* В России - согласно принятым методикам поверки (калибровки) средств измерений соответствующего типа.

Var(B) = Var(B₀) + Var(B₍₁₎) + Var(B₍₂₎) + …                                   (6)

Дисперсии обозначают следующим образом:

Var(B₀) = σ₍₀₎²;

Var(B₍₁₎) = σ₍₁₎²;

Var(B₍₂₎) = σ₍₂₎² и т.д.                                                    (7)

Var(B) оценивают на практике как s_L², и подобные же оценки промежуточной прецизионности могут быть получены на основании соответствующим образом поставленных экспериментов.

6.5 Составляющая погрешности e

6.5.1 Данная составляющая представляет случайную погрешность, имеющую место в каждом результате измерений, и процедуры, представленные в настоящем стандарте, разрабатывались при допущении, что распределение этой случайной величины является приближенно нормальным. Однако на практике их (процедуры) используют для большинства распределений при условии, что распределения являются унимодальными.

6.5.2 В пределах отдельно взятой лаборатории ее дисперсия носит название внутрилабораторной и ее выражают в виде

Var(e) = σ_W².                                                          (8)

6.5.3 Можно ожидать, что σ_W² будет иметь разные значения в разных лабораториях вследствие таких различий, как различия в квалификации операторов, однако в настоящем стандарте допускается, что для должным образом стандартизованного метода измерений такие различия между лабораториями должны быть невелики и это может быть оправданием для установления общего значения внутрилабораторной дисперсии для всех лабораторий, пользующихся этим методом. Это общее значение, которое оценивается средним значением внутрилабораторных дисперсий, называется «дисперсией повторяемости» и ее обозначают σ_r²:

                                                           (9)

Данное среднее значение берут по всем лабораториям, принимавшим участие в эксперименте по оценке точности и оставшимся после исключения выбросов.

7 Выбор условий измерений

7.1 При применении метода измерений в пределах лаборатории возможны многие условия измерений, а именно:

a) условия повторяемости (четыре фактора неизменны);

b) несколько промежуточных условий прецизионности с одним изменяющимся фактором;

c) несколько промежуточных условий прецизионности с двумя изменяющимися факторами;

d) несколько промежуточных условий прецизионности с тремя изменяющимися факторами;

e) промежуточные условия прецизионности с четырьмя изменяющимися факторами.

В стандарте на метод измерений нет необходимости (или даже возможности) устанавливать все возможные показатели прецизионности, хотя стандартное отклонение повторяемости должно определяться всегда. При выборе промежуточных мер прецизионности обычно встречающиеся условия должны определяться общей коммерческой практикой, и часто бывает достаточно задать всего лишь один соответствующий промежуточный показатель прецизионности с подробным описанием конкретных условий измерений, ассоциирующихся с ним. Значения влияющих факторов в условиях выполнения измерений, которые могут изменяться, должны быть точно определены; в частности, для промежуточных условий прецизионности с различием по фактору «время» должен быть задан практический средний интервал между последовательно выполняемыми измерениями.

7.2 Предполагается, что стандартизованный метод измерений будет иметь наименьшую систематическую погрешность и что эта систематическая погрешность, присущая самому методу, должна быть компенсирована техническими средствами. Поэтому в настоящем стандарте рассматривают только систематическую погрешность, обусловленную условиями измерений (см. 7.1).

7.3 Изменение в факторах условий измерений (время, калибровка, оператор и оборудование) по сравнению с условиями повторяемости (т.е. от состояния 1 в состояние 2 согласно таблице 1) увеличит изменчивость результатов измерений. Однако ожидаемое среднее значение ряда результатов измерений будет иметь меньшую систематическую погрешность по сравнению с систематической погрешностью в условиях повторяемости. Увеличение стандартного отклонения для промежуточных условий прецизионности можно преодолеть, не полагаясь на единичный результат измерений, а используя среднее значение нескольких результатов измерений в качестве окончательно приводимого результата.

7.4 На практике выбор факторов, влияние которых подлежит изучению при стандартизации метода измерений, будет зависеть как от желаемой прецизионности (стандартного отклонения) окончательного результата, так и от стоимости выполнения измерений.

8 Внутрилабораторное исследование и анализ промежуточных показателей прецизионности

8.1 Простейший подход

Простейший метод оценки стандартного отклонения промежуточной прецизионности в пределах одной лаборатории состоит в отборе одной пробы (или, для испытаний с разрушением образца, одного комплекта предположительно идентичных образцов) и выполнении серии из n измерений с изменением фактора(ов) между ними. Рекомендуется, чтобы n было не менее 15. Это может быть неприемлемо для лаборатории, и данный метод оценки промежуточных показателей прецизионности в пределах лаборатории не может быть признан эффективным в сравнении с другими процедурами. Анализ элементарен, однако и он может быть полезен для исследования промежуточной прецизионности с различием по фактору «время» путем выполнения последовательных измерений на одном и том же образце последовательно день за днем либо для исследования влияния фактора «калибровка» между измерениями.

Для идентификации потенциальных выбросов рекомендуется построить график  в функции номера измерения k, где y_k представляет собой k-й результат измерений из п повторных результатов, а  - среднее значение из n повторных результатов. Более формальная проверка выбросов состоит в применении критерия Граббса, как это представлено в 7.3.4 ГОСТ Р ИСО 5725-2.

Оценка стандартного отклонения промежуточной прецизионности при M изменяющихся факторов выражается в виде

                                              (10)

где в скобках должны быть проставлены символы, обозначающие промежуточные условия прецизионности.

8.2 Альтернативный метод

8.2.1 Альтернативный метод подразумевает t групп измерений, каждая из которых включает в себя n повторных результатов. Например, в одной лаборатории испытывают t материалов, после чего факторы промежуточной прецизионности изменяют и t материалов испытывают повторно, при этом процедуру повторяют до тех пор, пока не будет иметься в наличии n результатов измерений по каждому из t материалов. Каждая группа из n результатов измерений должна быть получена на одном идентичном образце или пробе (или на комплекте предположительно идентичных образцов или проб в случае испытаний с разрушением образцов), но при этом не требуется, чтобы материалы были идентичными. Необходимо только, чтобы все t материалов находились в таком диапазоне уровней испытаний (значений испытуемого параметра), в пределах которого можно использовать одно значение стандартного отклонения промежуточной прецизионности при M изменяющихся факторах. Рекомендуется, чтобы значение t(n - 1) было не менее 15.

Пример

Один оператор выполняет одно измерение на каждом из t материалов, после чего это повторяет второй оператор, а возможно, и третий оператор, и так далее, что позволяет рассчитать s_I(O).

8.2.2 Для идентификации потенциальных выбросов рекомендуется построить график  в функции номера материала j, где y_jk представляет собой k-й результат измерений, а  - среднее значение n результатов по j-му материалу. Более формальная проверка выбросов состоит в применении критерия Граббса, как это представлено в 7.3.4 ГОСТ Р ИСО 5725-2, либо для каждой группы в отдельности, либо для всех tn результатов измерений в совокупности.

Оценка стандартного отклонения промежуточной прецизионности при M изменяющихся факторах s_{I( )} в таком случае выражается в виде

                                           (11)

Для n = 2 (т.е. для двух результатов измерений по каждому материалу) формула упрощается, см. (12).

                                              (12)

8.3 Влияние условий измерений на окончательный результат

8.3.1 Полезность средних значений  лимитируется тем, что математическое ожидание различно для той или иной комбинации факторов - времени, калибровки, оператора и оборудования - даже в случае изменения только одного из них.

При химическом анализе или физических испытаниях значение  фиксируется в качестве окончательно приводимого результата. В торговле сырьем и материалами этот окончательно приводимый результат часто используют для оценки качества сырья и материалов, и он значительно влияет на цену продукции.

Пример

В международной торговле углем партия груза часто может превышать 70000 т, а зольность окончательно определяют в испытуемой навеске массой всего лишь 1 г. В договоре в особых условиях оговаривают, что расхождение в 1 % абсолютного содержания золы соответствует 1,5 долларов США за 1 т угля, поэтому расхождение в 1 мг при взвешивании золы на аналитических весах соответствует 0,1 % зольности, или 0,15 долларов США за 1 т, что для такой массы груза приводит к разнице в 10500 долларов США (0,1 ´ 1,5 ´ 70000).

8.3.2 Следовательно, окончательно приводимый результат химического анализа или физических испытаний должен быть достаточно точным, высоконадежным и, главное, универсальным и воспроизводимым. Окончательно приводимый результат, который может гарантироваться лишь в условиях выполнения измерений конкретным оператором, на конкретном оборудовании или в определенное время, может оказаться недостаточно удовлетворительным с коммерческой точки зрения.

9 Межлабораторное исследование и анализ промежуточных показателей прецизионности

9.1 Основные исходные положения

Оценка промежуточных показателей прецизионности путем межлабораторных исследований исходит из предпосылки, заключающейся в том, что влияние отдельного фактора одинаково во всех лабораториях, т.е., например, смена операторов в одной лаборатории имеет тот же самый эффект, что и смена операторов в другой лаборатории, или изменение, обусловленное фактором времени, одинаково во всех лабораториях. Если данная предпосылка нарушается, концепция промежуточных показателей прецизионности теряет смысл, так же, как лишаются смысла процедуры, предлагаемые в последующих разделах для их оценки. Нужно уделять повышенное внимание выбросам (речь идет не обязательно об исключении выбросов), так как это поможет обнаружить отклонения от исходных предпосылок, что необходимо при формировании информации от всех лабораторий для последующих расчетов. Одним из действенных приемов обнаружения потенциальных выбросов является графическое изображение результатов измерений как функции различных уровней факторов или различных лабораторий участников исследования.

9.2 Простейший подход

Если материал на q уровнях рассылается в p лабораторий, каждая из которых выполняет измерения на каждом из q уровней с изменением фактора(ов) промежуточной прецизионности в интервалах между каждыми из n измерений, то анализ проводят с помощью того же метода расчета, который изложен в ГОСТ Р ИСО 5725-2, за исключением того, что вместо стандартного отклонения повторяемости оценивают стандартное отклонение промежуточной прецизионности.

9.3 Вложенные эксперименты

Следующим способом оценки промежуточных показателей прецизионности является проведение более сложных экспериментов. Это могут быть полностью или ступенчато вложенные эксперименты (определения данных терминов см. в ИСО 3534-3 [4]). Преимущество использования экспериментов вложенного типа состоит в том, что имеется возможность в одно время и в одном межлабораторном эксперименте оценить не только стандартные отклонения повторяемости и воспроизводимости, но и одно или большее число стандартных отклонений промежуточной прецизионности. Существуют, однако, определенные предостережения, которые должны приниматься во внимание, и они будут разъяснены в 9.8.

9.4 Полностью вложенный эксперимент

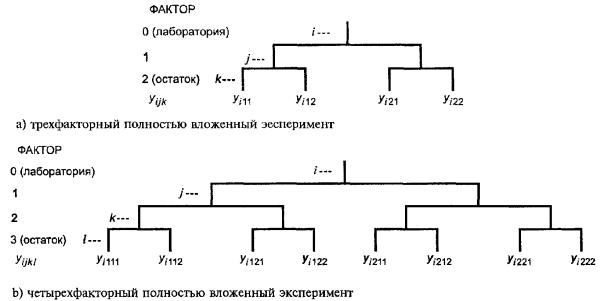
Схематическое изображение полностью вложенного эксперимента на определенном уровне испытаний представлено на рисунке 1.

Посредством выполнения трехфакторного полностью вложенного эксперимента сообща в нескольких лабораториях может быть получен один промежуточный показатель прецизионности в одно и то же время со стандартными отклонениями повторяемости и воспроизводимости, т.е. могут быть оценены σ₍₀₎, σ₍₁₎ и σ_r. Аналогично четырехфакторный полностью вложенный эксперимент может быть использован для получения двух промежуточных показателей прецизионности, т.е. могут быть оценены σ₍₀₎, σ₍₁₎ σ₍₂₎ и σ_r.

Подстрочные индексы i, j и k при y на рисунке 1a) для трехфакторного полностью вложенного эксперимента представляют, например, лабораторию, день проведения эксперимента и номер результата для n измерений, проведенных в условиях повторяемости для каждой комбинации i и j.

Подстрочные индексы i, j, k и l при y на рисунке 1b) для четырехфакторного полностью вложенного эксперимента представляют, например, лабораторию, день проведения эксперимента, оператора и номер результата для n измерений, проведенных в условиях повторяемости для каждой комбинации i, j, k.

Рисунок 1 - Схемы трех- и четырехфакторных полностью вложенных экспериментов

Анализ результатов многофакторного полностью вложенного эксперимента осуществляют по методике «анализ дисперсии» (ANOVA) отдельно для каждого уровня испытаний, он детально описан в приложении В.

9.5 Ступенчато вложенный эксперимент

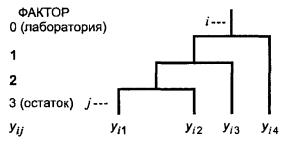
Схематическое изображение ступенчато вложенного эксперимента для определенного уровня испытаний представлено на рисунке 2.

Рисунок 2 - Схема четырехфакторного ступенчато вложенного эксперимента

Трехфакторный ступенчато вложенный эксперимент требует от каждой лаборатории i получения трех результатов измерений. Результаты измерений y_i1 и y_i2 должны быть получены в условиях повторяемости, а y_i3 - при каком-либо из промежуточных условий прецизионности с M изменяющимися факторами (M = 1, 2 или 3), например при условии различия во времени (посредством получения у_i3 в другой день по сравнению с днем, когда были получены y_i1 и y_i2).

При четырехфакторном ступенчато вложенном эксперименте результат y_i4 должен быть получен при другом промежуточном условии прецизионности с дополнительным изменяющимся фактором, например при условии различия по факторам (время + оператор) посредством смены дня проведения эксперимента и оператора.

Опять же, анализ результатов многофакторного ступенчато вложенного эксперимента осуществляют по методике «анализ дисперсии» (ANOVA) отдельно для каждого уровня испытаний, и он детально описан в приложении С.

9.6 Распределение факторов в схеме вложенного эксперимента

Факторы в схеме вложенного эксперимента распределяют так, чтобы факторы, испытывающие по большей части влияние систематических эффектов, располагались на высших рангах (0, 1, …), а факторы, подверженные в большей мере влиянию случайных эффектов, располагались на низших рангах; самым низшим фактором считают остаточную вариацию (повторы). Например, в четырехфакторной схеме (см. рисунки 1b и 2) фактор 0 мог бы быть лабораторией, фактор 1 - оператором, фактор 2 - днем выполнения измерения, а фактор 3 - количеством параллельных определений. Это может оказаться несущественным в случае полностью вложенного эксперимента по причине его симметрии.

9.7 Сопоставление схемы вложенного эксперимента со схемой, представленной в ГОСТ Р ИСО 5725-2

Поскольку в эксперименте, описанном в ГОСТ Р ИСО 5725-2, анализ проводят по отдельности для каждого уровня испытаний (материала), он фактически представляет собой двухфакторный полностью вложенный эксперимент и дает в результате два стандартных отклонения: повторяемости и воспроизводимости. Фактор 0 представляет собой лабораторию, а фактор 1 - количество параллельных определений. Если в такую схему ввести еще один фактор, к примеру - двух операторов в каждой лаборатории, получающих каждый по два результата измерения в условиях повторяемости, то в таком случае, в дополнение к стандартным отклонениям повторяемости и воспроизводимости, можно было бы определить стандартное отклонение промежуточной прецизионности с различающимся фактором оператора. Или же если бы каждая лаборатория пользовалась услугами только одного оператора, но повторяла бы эксперимент в другой день, то посредством данного трехфакторного полностью вложенного эксперимента можно было бы определить стандартное отклонение промежуточной прецизионности с изменяющимся фактором времени. Дополнение эксперимента еще одним фактором, таким, что каждая лаборатория имела бы двух операторов, каждый из которых выполнял бы по два измерения, а эксперимент в целом повторялся бы на следующий день, позволило бы определить не только стандартные отклонения повторяемости и воспроизводимости, но и стандартные отклонения прецизионности с изменяющимися факторами оператора, времени [время + оператор].

9.8 Сопоставление схем полностью вложенного и ступенчато вложенного экспериментов

n-Факторный полностью вложенный эксперимент требует от каждой лаборатории 2^n-1 результатов измерений, что может оказаться чрезмерным. Это главный аргумент в пользу схемы ступенчато вложенного эксперимента. Он требует меньшего количества результатов измерений для получения тех же стандартных отклонений ценой большей неопределенности в их оценках и некоторого усложнения анализа.

ПРИЛОЖЕНИЕ A

(обязательное)

Условные обозначения и сокращения, используемые в ГОСТ Р ИСО 5725

a                          Отсекаемый на оси ординат отрезок в соотношении s = a + bm

A                          Показатель, используемый для расчета неопределенности оценки

b                          Угловой коэффициент прямой в соотношении s = a + bm

B                          Лабораторная составляющая систематической погрешности измерений при реализации конкретного метода - разность между систематической погрешностью лаборатории при реализации конкретного метода измерений (конкретной МВИ) и систематической погрешностью метода измерений

B₀                                         Составляющая величины B, представляющая все факторы, которые не изменяются в условиях промежуточной прецизионности

B₍₁₎, B₍₂₎ и т.д.      Составляющие величины B, представляющие факторы, которые изменяются в условиях промежуточной прецизионности

c                           Отсекаемый на оси ординат отрезок в соотношении lgs = c + d·lgm

C, C', C"              Тестовые статистики

C_crit, C'_crit, C"_crit  Критические значения для статистик

CD_P                     Критическая разность для вероятности P

CR_P                      Критический диапазон для вероятности P

d                          Угловой коэффициент прямой в соотношении lgs = c + d·lgm

e                           Составляющая результата измерений, представляющая случайную погрешность каждого результата измерений

f                           Коэффициент критического диапазона

F_p(ν₁, ν₂)              p-квантиль F-распределения с ν₁ и ν₂ степенями свободы

G                          Статистика Граббса

h                          Статистика Манделя для межлабораторной совместимости

k                           Статистика Манделя для внутрилабораторной совместимости

LCL                     Нижний предел контроля (действия либо предупреждения)

m                          Общее среднее значение измеряемой характеристики; уровень

M                         Количество факторов, рассматриваемых в условиях промежуточной прецизионности

N                          Количество повторений (итераций)

n                          Количество результатов измерений, полученных в одной лаборатории на одном уровне (т.е. в пределах ячейки - базового элемента)

p                          Количество лабораторий, участвующих в межлабораторном эксперименте

P                          Вероятность

q                          Количество уровней измеряемой характеристики в межлабораторном эксперименте

r                           Предел повторяемости (сходимости)

R                          Предел воспроизводимости

RM                      Стандартный образец

s                           Оценка стандартного (среднеквадратического) отклонения

                         Прогнозируемое стандартное (среднеквадратическое) отклонение

T                          Итог или сумма какого-либо выражения

t                           Количество объектов испытаний или групп объектов

UCL                     Верхний предел контроля (действия либо предупреждения)

W                         Весовой коэффициент, используемый при расчете взвешенной регрессии

w                          Диапазон изменения выборки результатов измерений

x                           Заданная величина, используемая для критерия Граббса

y                           Результат измерений (или результат испытаний)

                         Среднее арифметическое значение результатов измерений (или результатов испытаний)

                         Общее среднее значение результатов измерений (или результатов испытаний)

α                          Уровень значимости

β                          Вероятность ошибки второго рода

γ                           Отношение стандартного отклонения воспроизводимости к стандартному отклонению повторяемости (сходимости) (σ_R/σ_r)

Δ                          Систематическая погрешность лаборатории при реализации конкретного стандартного метода измерений (конкретной МВИ)

                        Оценка Δ

δ                          Систематическая погрешность метода измерений

                         Оценка δ

λ                          Поддающаяся обнаружению разность между систематическими погрешностями двух лабораторий при реализации одного и того же метода измерений или систематическими погрешностями двух методов измерений (МВИ) одного и того же назначения на идентичных образцах

μ                          Истинное или принятое опорное значение измеряемой величины (характеристики)

ν                           Число степеней свободы

ρ                          Поддающееся обнаружению соотношение между стандартными отклонениями повторяемости (сходимости) для методов В и А

σ                          Истинное (действительное) значение стандартного отклонения

τ                           Составляющая результата измерений, представляющая изменение, обусловленное временем, прошедшим с момента последней калибровки

φ                          Поддающееся обнаружению соотношение между квадратными корнями из межлабораторных средних квадратов для методов В и А

σ²_M                       p-квантиль χ²-распределения с ν степенями свободы

Символы, используемые в качестве подстрочных индексов

C                          Различие, определяемое калибровкой

E                          Различие, определяемое оборудованием

i                           Идентификатор для конкретной лаборатории

I( )                       Идентификатор для промежуточных мер прецизионности; в скобках - идентификация типа промежуточной ситуации

j                           Идентификатор для уровня (ГОСТ Р ИСО 5725-2)

Идентификатор для группы испытаний или для фактора (ГОСТ Р ИСО 5725-3)

k                           Идентификатор для конкретного результата испытаний в лаборатории i на уровне j

L                          Межлабораторный

m                          Идентификатор для поддающейся обнаружению систематической погрешности

M                         Различие, обусловленное неидентичностью проб (образцов)

O                          Различие, определяемое сменой оператора

P                          Вероятность

r                           Повторяемость

R                          Воспроизводимость

T                          Различие, обусловленное периодом (временем), в течение которого проводят измерения или оценочный эксперимент

W                         Внутрилабораторный

1, 2, 3, …            Для результатов измерений, нумеруемых в порядке их получения

(1), (2), (3), …    Для результатов измерений (или результатов испытаний), нумеруемых в порядке возрастания измеряемой величины

ПРИЛОЖЕНИЕ B

(обязательное)

Анализ дисперсии для полностью вложенных экспериментов

Анализ дисперсии, описываемый в настоящем приложении, должен проводиться по отдельности для каждого уровня испытаний, предусмотренного в межлабораторном эксперименте. Для упрощения у данных опущен подстрочный индекс, указывающий на уровень испытаний. Отметим, что в настоящем стандарте подстрочный индексу используют для обозначения фактора 1 (фактор 0 означает лабораторию), в то время как в других частях ГОСТ Р ИСО 5725 его используют для обозначения уровня испытаний.

Для проверки данных на совместимость и наличие выбросов должны применяться методы, описанные в 7.3 ГОСТ Р ИСО 5725-2. Для экспериментов, описываемых в настоящем приложении, точный анализ данных очень сложен в случаях, когда опускаются отдельные результаты измерений, получаемые от лаборатории. Поэтому если принимают решение о том, что некоторые результаты являются квазивыбросами или выбросами и должны быть исключены из анализа, то рекомендуется исключить также все другие данные, полученные лабораторией на уровнях, где имеются исключаемые квазивыбросы и выбросы.

В.1 Трехфакторный полностью вложенный эксперимент

Данные, полученные в результате эксперимента, обозначают через y_ijk, а средние значения и диапазоны изменений имеют следующий вид:

               

             

где p - количество лабораторий, участвовавших в межлабораторном эксперименте.

Полную сумму квадратов SST можно подразделить следующим образом:

где

Поскольку число степеней свободы для сумм квадратов SS0, SS1 и SSe составляет соответственно p - 1, p и 2p, таблица для анализа дисперсии ANOVA имеет следующий вид (см. таблицу В.1).

Таблица В.1 - Анализ ANOVA для трехфакторного полностью вложенного эксперимента

Из средних квадратов MS0, MS1 и MSe могут быть получены несмещенные оценки s²₍₀₎, s²₍₁₎ и s²_r соответствующих величин σ²₍₀₎, σ²₍₁₎ и σ²_r, а именно:

s²₍₀₎ = 1/4(MS0 - MS1),

s²₍₁₎ = 1/2(MS1 - MSe),

s²_r = MSe.

Оценки дисперсий повторяемости, промежуточной прецизионности с одним изменяющимся фактором и воспроизводимости соответственно равны:

s²_r,

s²_I(1) = s²_r + s²₍₁₎,

s²_R = s²_r + s²₍₁₎ + s²₍₀₎.

В.2 Четырехфакторный полностью вложенный эксперимент

Данные, полученные в результате эксперимента, обозначают y_ijkl, а средние значения и диапазоны изменений имеют следующий вид:

          

             

               

где p - количество лабораторий, участвовавших в межлабораторном эксперименте. Полную сумму квадратов SST можно подразделить следующим образом:

где

Поскольку число степеней свободы для сумм квадратов SS0, SS1, SS2 и SSe составляет соответственно p - 1, p, 2p и 4p, таблица для анализа дисперсии ANOVA имеет следующий вид (см. таблицу В.2).

Таблица В.2 - Таблица ANOVA для четырехфакторного полностью вложенного эксперимента

Из средних квадратов MS0, MS1, MS2 и MSe могут быть получены несмещенные оценки s²₍₀₎, s²₍₁₎, s²₍₂₎ и s²_r соответствующих величин σ²₍₀₎, σ²₍₁₎, σ²₍₂₎, и σ²_r, а именно:

s²₍₀₎ = 1/8(MS0 - MS1),

s²₍₁₎ = 1/4(MS1 - MS2),

s²₍₂₎ = 1/2(MS2 - MSe),

s²_r = MSe.

Оценки дисперсий повторяемости, промежуточной прецизионности с одним изменяющимся фактором, промежуточной прецизионности с двумя изменяющимися факторами и воспроизводимости соответственно равны:

s²_r,

s²_I(1) = s²_r + s²₍₂₎,

s²_I(2) = s²_r + s²₍₂₎ + s²₍₁₎,

s²_R = s²_r + s²₍₂₎ + s²₍₁₎ + s²₍₀₎.

ПРИЛОЖЕНИЕ C

(обязательное)

Анализ дисперсии для ступенчато вложенных экспериментов

Анализ дисперсии, описываемый в настоящем приложении, должен проводиться по отдельности для каждого уровня испытаний, предусмотренного в межлабораторном эксперименте. Для упрощения у данных опущен подстрочный индекс, указывающий на уровень испытаний. Отметим, что в настоящем стандарте подстрочный индекс j используют для обозначения параллельных определений в лаборатории, в то время как в других частях ГОСТ Р ИСО 5725 его используют для обозначения уровня испытаний.

Для проверки данных на совместимость и наличие выбросов должны применяться методы, описанные в 7.3 ГОСТ Р ИСО 5725-2. Для экспериментов, описываемых в настоящем приложении, точный анализ данных очень сложен в случаях, когда опускаются отдельные результаты измерений, получаемые от лаборатории. Поэтому если принимают решение о том, что некоторые результаты измерений лаборатории являются квазивыбросами или выбросами и должны быть исключены из анализа, то рекомендуется исключить также все другие данные, полученные этой лабораторией на уровнях, где имеются исключаемые квазивыбросы и выбросы.

С.1 Трехфакторный ступенчато вложенный эксперимент

Данные, полученные в результате эксперимента в пределах лаборатории i, обозначают y_ij (j = 1, 2, 3), а средние значения и диапазоны изменений имеют следующий вид:

где p - количество лабораторий, участвовавших в межлабораторном эксперименте.

Полную сумму квадратов SST можно подразделить следующим образом:

где

Поскольку число степеней свободы для сумм квадратов SS0, SS1 и SSe составляет соответственно p - 1, p и p, таблица ANOVA для анализа дисперсии имеет следующий вид (см. таблицу С.1).

Таблица С.1 - Анализ ANOVA для трехфакторного ступенчато вложенного эксперимента

Из средних квадратов MS0, MS1 и MSe могут быть получены несмещенные оценки s²₍₀₎, s²₍₁₎, и s²_(r) соответствующих величин σ²₍₀₎, σ²₍₁₎, и σ²_(r), а именно:

s²₍₀₎ = 1/3MS0 - 5/12MS1 + 1/12MSe,

s²₍₁₎ = 3/4MS1 - 3/4MSe,

s²_r = MSe.

Оценки дисперсий повторяемости, промежуточной прецизионности с одним изменяющимся фактором и воспроизводимости соответственно равны:

s²_r,

s²_I(1) = s²_r + s²₍₁₎,

S²_R = S²_r + S²₍₁₎ + S²₍₀₎.

С.2 Четырехфакторный ступенчато вложенный эксперимент

Данные, полученные в результате эксперимента в пределах лаборатории i, обозначают y_ij (j = 1, 2, 3, 4), а средние значения и диапазоны изменений имеют следующий вид:

где p - количество лабораторий, участвовавших в межлабораторном эксперименте.

Таблица для анализа дисперсии (ANOVA) имеет следующий вид (см. таблицу С.2)

Таблица С.2 - Анализ ANOVA для четырехфакторного ступенчато вложенного эксперимента

С.3 Пятифакторный ступенчато вложенный эксперимент

Данные, полученные в результате эксперимента в пределах лаборатории i, обозначают y_ij (j = 1, 2, 3, 4, 5), а средние значения и диапазоны изменений имеют следующий вид:

где p - количество лабораторий, участвовавших в межлабораторном эксперименте.

Таблица для анализа дисперсии (ANOVA) имеет следующий вид (см. таблицу С.3).

Таблица С.3 - Анализ ANOVA для пятифакторного ступенчато вложенного эксперимента

С.4 Шестифакторный ступенчато вложенный эксперимент

Данные, полученные в результате эксперимента в пределах лаборатории i, обозначают y_ij (j = 1, 2, 3, 4, 5, 6), а средние значения и диапазоны изменений имеют следующий вид:

где p - количество лабораторий, участвовавших в межлабораторном эксперименте

Таблица для анализа дисперсии (ANOVA) имеет следующий вид (см. таблицу С.4).

Таблица С.4 - Анализ ANOVA для шестифакторного ступенчато вложенного эксперимента

ПРИЛОЖЕНИЕ D

(справочное)

Примеры статистического анализа данных экспериментов по оценке промежуточных показателей прецизионности

D.1 Пример 1. Получение стандартного отклонения S_I(TO) промежуточных показателей прецизионности с изменяющимися факторами [время + оператор] в пределах определенной лаборатории на отдельном уровне

D.1.1 Сведения общего характера

a) Метод измерений

Определение содержания углерода в стали методом вакуумно-эмиссионной спектрометрии. Результаты измерений выражены в процентах по массе.

b) Источник

Регулярный отчет сталеплавильного завода за ноябрь 1984 г.

c) План эксперимента

В определенной лаборатории проба, отобранная наугад из материалов, анализировавшихся в один день, снова была проанализирована на следующий день другим аналитиком. За месяц было получено 29 пар такого рода данных (см. таблицу D.1).

Таблица D.1 - Исходные данные. Содержание углерода, % по массе

D.1.2 Анализ

Данные y_j1, y_j2 и w_j = |y_j1 - y_j2| представлены в таблице D.1. Анализ проводился по методике, изложенной в 8.2.

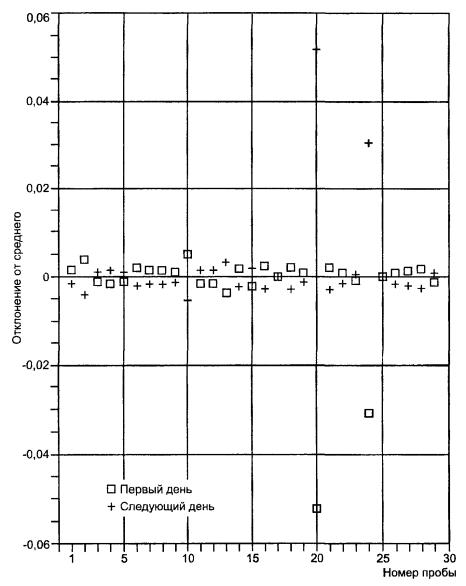
На рисунке D.1 представлена диаграмма отклонений от средних значений, полученных в первый и второй дни в функции номера пробы j. Диаграмма и применение критерия Кохрена указывают, что расхождения (диапазоны изменений) для проб с номерами 20 и 24 являются выбросами. Такое большое расхождение вероятнее всего обусловлено ошибками при регистрации данных. Значения, соответствующие этим пробам, были изъяты из выполненного по формуле (12) расчета стандартного отклонения s_I(TO) промежуточной прецизионности с изменяющимися факторами (время + оператор), которое оказалось равным

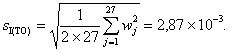
Рисунок D.1 - Содержание углерода в стали. Отклонения от среднего значения результатов измерений, полученных в первый и второй дни, для различных проб

D.2 Пример 2. Получение стандартного отклонения промежуточной прецизионности с изменяющимся фактором времени посредством межлабораторного эксперимента

D.2.1 Сведения общего характера

a) Метод измерений

Определение содержания ванадия в стали методом атомно-абсорбционной спектрометрии, описанным в инструкции к эксперименту. Результаты исследования выражают в процентах по массе.

b) Источник

ИСО/ТК 17 Сталь/ПК 1, Методы определения химического состава. Эксперимент проводился в мае 1985 г.

c) Схема эксперимента.

Трехфакторный ступенчато вложенный эксперимент осуществлялся с участием 20 лабораторий, каждая из которых представляла два результата измерений в условиях повторяемости в первый день и еще один результат - на следующий день на каждом из шести уровней, предусмотренных в эксперименте. Все измерения в каждой лаборатории выполнялись одним оператором, с использованием одного и того же измерительного оборудования.

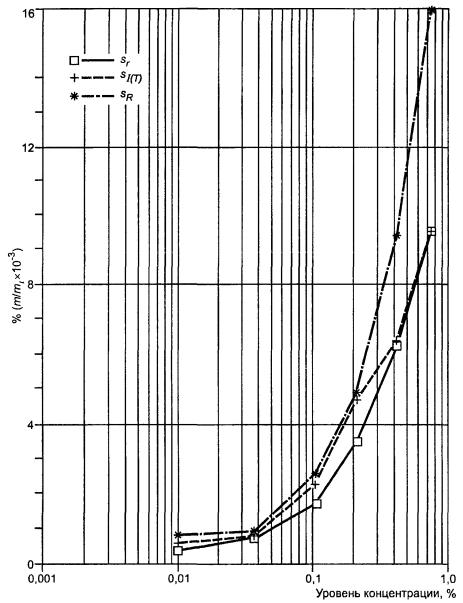
D.2.2 Анализ

Данные для всех шести уровней представлены в таблице D.2.

Рисунок D.2 - Содержание ванадия в стали. Результаты измерений, полученные в первый и второй дни на уровне 1 в различных лабораториях

Анализ дисперсии дается только для одного из уровней, а именно для уровня 1.

Диаграмма данных (результаты измерений, проводимых в первый и второй дни в функции номера лаборатории i) приведена на рисунке D.2. Диаграмма свидетельствует о том, что лаборатория 20 - выпадающая. Имеет место большое расхождение между результатом измерений во второй день и средним значением в первый день по сравнению с результатами измерений в других лабораториях. Данная лаборатория была исключена из расчетов показателей прецизионности.

В соответствии с С.1 приложения C были рассчитаны значения w_i(1), w_i(2), , и результаты представлены в таблице D.3.