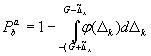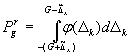Федеральное государственное унитарное предприятие
Всероссийский научно-исследовательский институт
метрологической службы (ВНИИМС)
РЕКОМЕНДАЦИЯ
Государственная система обеспечения единства измерений.
Результаты и характеристики погрешности измерений.
Формы представления. Способы использования при испытаниях
образцов продукции и контроле их параметров
МИ 1317-2004
Москва, 2004
Разработана Федеральным государственным унитарным предприятием Всероссийский научно-исследовательский институт метрологической службы (ФГУП ВНИИМС)
Исполнители
М.А. Земельман, канд. техн. наук (руководитель темы); В.Г. Цейтлин, канд. техн. наук; В.М. Кашлаков, канд. техн. наук; В.П. Кузнецов, канд. техн. наук; Н.П. Миф, канд. техн. наук; В.А. Брюханов, канд. техн. наук; В.И. Гронский, канд. техн. наук; И.М. Тронова
Утверждена ФГУП ВНИИМС 20 декабря 2004 г.
Зарегистрирована ФГУП ВНИИМС 28 декабря 2004 г.
Взамен МИ 1317-86
CОДЕРЖАНИЕ
РЕКОМЕНДАЦИИ
|
Государственная система обеспечения единства измерений. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров |
МИ 1317 - 2004 |
Настоящая рекомендация распространяется на нормативные, методические и технические документы (проектно-конструкторскую и технологическую документацию, стандарты, технические условия, технические задания, отчеты, протоколы, программы, документы на методики испытаний и контроля образцов продукции, руководящие документы, руководящие технические материалы, документы на методики выполнения измерений), техническую литературу, в которых указывают требования к измерениям или описывают измерения, проводимые в научных исследованиях; при разработке, производстве, эксплуатации продукции; при охране окружающей природной среды; в здравоохранении и др.
Рекомендация устанавливает формы представления результатов измерений, характеристики погрешности измерений и формы их представления для всех возможных случаев применения, а также способы использования характеристик погрешности измерений для определения характеристик погрешности таких испытаний и достоверности такого контроля параметров образцов (проб) продукции, которые проводят с помощью измерений.
В рекомендации использованы ссылки на следующие нормативные документы:
ГОСТ 8.009-84 Государственная система обеспечения единства измерений. Нормируемые метрологические характеристики средств измерений;
ГОСТ Р 8.563-96 Государственная система обеспечения единства измерений. Методики выполнения измерений;
РД 50-453-84 Государственная система обеспечения единства измерений. Характеристики погрешности средств измерений в реальных условиях эксплуатации. Методы расчета;
РМГ 29-99 Государственная система обеспечения единства измерений. Метрология. Основные термины и определения.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1 Непосредственной целью измерений является определение истинных значений постоянной или изменяющейся измеряемой величины. Результат измерений является реализацией случайной величины, равной сумме истинного значения измеряемой величины и погрешности измерений.
Примечание - В качестве измеряемых величин принимают параметры модели объекта измерений. Общие рекомендации по выбору измеряемых величин даны в приложении А.
1.2 Термины "результат измерений" и "погрешность измерений" - в соответствии с РМГ 29.
1.3 Наименьшие разряды числовых значений результатов измерений принимают такими же, как и наименьшие разряды числовых значений среднего квадратического отклонения абсолютной погрешности измерений или числовых значений границ, в которых находится абсолютная погрешность измерений (или статистических оценок этих характеристик погрешности).
1.4 В качестве функции плотности распределения вероятностей погрешности измерений принимают закон, близкий к нормальному усеченному, если имеются основания предполагать, что реальная функция плотности распределения функция симметричная, одномодальная, отличная от нуля на конечном интервале значений аргумента, и другая информация о плотности распределения отсутствует.
1.4.1 Если имеется информация о том, что хотя бы одно из указанных в 1.4 условий не выполнено, принимают другую аппроксимацию функции плотности распределения вероятностей погрешности измерений, более соответствующую решаемой измерительной задаче.
1.4.2 В качестве функции плотности распределения вероятностей составляющих погрешности измерений, для которых известны только пределы допускаемых значений, т.е. границы интервала, в пределах которых находится соответствующая составляющая погрешности измерений с вероятностью 1, при расчетах характеристик погрешности измерений принимают закон равномерной плотности, если отсутствует информация об ином виде распределения.
1.5 Для расчета характеристик погрешности измерений при проектировании или аттестации методик выполнения измерений (далее - МВИ) по ГОСТ Р 8.563 в общем случае используют:
- метрологические характеристики средств измерений, нормированные по ГОСТ 8.009;
- характеристики влияющих величин, определяющие условия измерений, в частности, условия применения средств измерений;
- характеристики объекта измерений, влияющие на погрешность измерений.
1.6 Наряду с указанными в настоящей рекомендации можно использовать характеристики погрешности измерений, которые являются функциями характеристик, приведенных в разделе 2.
1.7 Основные обозначения, принятые в настоящей рекомендации, приведены в приложении В.
2 ХАРАКТЕРИСТИКИ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
2.1 Настоящая рекомендация устанавливает следующие группы характеристик погрешности измерений:
2.1.1 Задаваемые в качестве требуемых или допускаемых - нормы характеристик погрешности измерений (нормы погрешности измерений).
2.1.2 Приписываемые любому результату измерений из совокупности результатов измерений, выполняемых по одной и той же аттестованной МВИ - приписанные характеристики погрешности измерений.
2.1.3 Отражающие близость отдельного, экспериментально полученного результата измерений к истинному значению измеряемой величины статистические оценки характеристик погрешности измерений (статистические оценки погрешности измерений).
2.2 При массовых технических измерениях, выполняемых при технологической подготовке производства, в процессах разработки, испытаний, производства, контроля и эксплуатации (потребления) продукции, при товарообмене, торговле и др., преимущественно применяют нормы погрешности измерений, а также приписанные характеристики погрешности измерений (по 2.1.1 и 2.1.2). Они представляют собой вероятностные характеристики (характеристики генеральной совокупности) случайной величины - погрешности измерений.
2.3 При измерениях, выполняемых при проведении научных исследований и метрологических работ (определение физических констант, свойств и состава стандартных образцов, индивидуальном исследовании средств измерений и т. п.), преимущественно применяют статистические оценки погрешности измерений (по 2.1.3.). Они представляют собой статистические (выборочные) характеристики случайной величины - погрешности измерений.
2.4 Рекомендация устанавливает следующие альтернативные вероятностные и статистические характеристики погрешности измерений:
среднее квадратическое отклонение погрешности измерений;
границы, в пределах которых погрешность измерений находится с заданной вероятностью;
характеристики случайной и систематической составляющих погрешности измерений.
Примечание:
1 Возможны случаи, когда границам погрешности измерений приписывают вероятность, равную единице.
2 Математическое ожидание погрешности измерений не рассматривают в качестве характеристики погрешности измерений, так как оно представляет собой систематическую погрешность, и если ее значение известно, то на нее в результат измерений вводят поправку.
2.4.1 В качестве характеристик случайной составляющей погрешности измерений используют: среднее квадратическое отклонение случайной составляющей погрешности измерений и (при необходимости) нормализованную автокорреляционную функцию случайной составляющей погрешности измерений или характеристики этой функции.
2.4.2 В качестве характеристик систематической составляющей погрешности измерений используют: среднее квадратическое отклонение неисключенной систематической составляющей погрешности измерений или границы, в которых неисключенная систематическая составляющая погрешности измерений находится с заданной вероятностью (в частности, с вероятностью, равной единице).
2.5 Характеристики погрешности измерений по 2.1.1, 2.1.2, 2.1.3. приведены в таблице 1.
2.6 При необходимости средние квадратические отклонения случайной и (или) неисключенной систематической составляющих погрешности измерений сопровождают указанием принятой аппроксимации закона распределения вероятностей погрешности или его качественным описанием (например, симметричный, одномодальный и т.п.).
2.7 В случаях, когда результаты измерений (испытаний) используют (могут быть использованы) совместно с другими результатами измерений, а также при расчетах погрешностей величин, функционально связанных с результатами измерений (например, критериев эффективности, функций потерь, результатов косвенных измерений и др.), в качестве характеристик погрешности измерений применяют, в основном, точечные характеристики погрешности - средние квадратические отклонения погрешности.
В случаях, когда результаты измерений являются окончательными, пригодными для решения определенной технической задачи и не предназначены для совместного использования с другими результатами измерений и для расчетов, применяют, в основном, интервальные характеристики погрешности - границы, в пределах которых погрешность находится с известной (заданной) вероятностью.
Примеры к 2.7:
Пример 1 - Требования к погрешности измерений задают с целью ограничения потерь, вызываемых этой погрешностью. Функция потерь, вызванных погрешностью измерений, имеет квадратичный или V-образный вид. В этом случае погрешность измерений целесообразно задавать допускаемым значением среднего квадратического отклонения, т. к. именно эта характеристика однозначно связана с потерями (с математическим ожиданием потерь) независимо от вида распределения погрешности измерений.
Пример 2 - Оцениваемую погрешность измерений текущих (мгновенных) значений изменяющейся измеряемой величины используют для расчета погрешности средних величин или технико-экономических показателей за различные интервалы времени. В этом случае целесообразно оценивать следующие характеристики погрешности измерений текущих значений: среднее квадратическое отклонение случайной составляющей и интервал корреляции автокорреляционной функции этой составляющей, а также среднее квадратическое отклонение неисключенной систематической составляющей. Оценки таких характеристик дают возможность учесть влияние интервала времени усреднения и числа наблюдений на случайную составляющую погрешности средних значений.
|
Характеристики погрешности измерений |
Нормы (по 2.1.1) |
Приписанные (по 2.1.2) |
Статистические оценки (по 2.1.3.) |
|
1 |
2 |
3 |
4 |
|
Среднее квадратическое отклонение погрешности измерений |
Предел допускаемых значений σр[Δ] |
Наибольшее возможное значение σm[Δ] |
Оценка ỡ[Δ] и (в случае необходимости) нижняя ỡl[Δ] и верхняя ỡh[Δ] границы доверительного интервала, доверительная вероятность РдовΔ |
|
Границы, в которых погрешность измерений находится с заданной вероятностью |
Нижняя ΔР1 и верхняя Δрh, границы допускаемого интервала, вероятность Р |
Нижняя Δl и верхняя Δh, границы интервала, вероятность Р |
Оценка нижней Δ̃1 и верхней Δ̃h, границ интервала, вероятность Р |
|
Характеристики случайной составляющей погрешности измерений: среднее квадратическое отклонение |
Предел
допускаемых значений σρ[ |
Наибольшее
возможное значение σm [ |
Оценка
ỡ |
|
Нормализованная автокорреляционная функция Характеристики нормализованной автокорреляционной функции (например, интервал корреляции) |
Нормализованная
функция Нижний и (или) верхний пределы допускаемых значений характеристики |
Приписанная
функция Наибольшее и (или) наименьшее возможные значения характеристики |
Оценка
функции Оценка характеристики |
|
Характеристики неисключенной систематической составляющей погрешности измерений: |
|
|
|
|
среднее квадратическос отклонение неисключенной систематической составляющей |
Предел допускаемых значений σp[Δs] |
Наибольшее возможное значение σм[Δs] |
Оценка ỡ[Δs] и (в случае необходимости) нижняя σl[Δs] и верхняя σh[Δs] границы доверительного интервала, доверительная вероятность Рдов.s |
|
границы, в которых неисключенная систематическая составляющая находится с заданной вероятностью |
Нижняя Δspl и верхняя Δsph границы допускаемого интервала, вероятность Ps |
Нижняя Δsl и верхняя границы интервала, вероятность Ps |
Оценка нижней Δ̃sl и верхней границ Δ̃sh интервала, вероятность Ps |
Примечания к таблице 1
1.При одинаковых числовых значениях (без учета знаков) нижних и верхних границ характеристик погрешности указывают одно числовое значение, ставя перед ним знаки ±. В противном случае границы указывают отдельно каждую со своим знаком.
2.В таблице приведены обозначения для характеристик абсолютной погрешности измерений. Для обозначения характеристик относительной погрешности измерений букву Δ заменяют на δ (в том числе в индексах).
3 Рекомендуемое значение вероятности (доверительной вероятности) Р=0,95.
4.Пределы допускаемых значений характеристик погрешности определяют интервал, в котором находится данная характеристика, т.е. они соответствуют вероятности нахождения характеристики в данном интервале, равной единице.
5.Если вероятность, для которой нормированы границы допускаемого интервала погрешности измерений (графа 2), равна единице (Р=1), т.е. ни одна из реализаций погрешности измерений не должна выходить за эти границы, то их можно называть пределами допускаемых значений и при этом вероятность Р=1 не указывать.
Пример 3 - Определяют уставки технологической защиты, срабатывающей, когда результат однократного измерения превышает значение уставки. В этом случае для представления о возможности неблагоприятных последствий ограниченной точности измерений (ложного срабатывания или несрабатывания в аварийной ситуации) учитывают границы погрешности измерений. Для подобного учета погрешность измерений целесообразно задавать границами допускаемых значений с заданной вероятностью.
2.8. При условиях, приведенных в 1.4, расчет интервальных характеристик погрешности измерений для заданных вероятностей, меньших единицы, по среднему квадратическому отклонению погрешности может быть проведен в соответствии с приложением Б.
Методика, изложенная в приложении Б, основана на использовании вместо неизвестного реального закона распределения вероятностей погрешности (удовлетворяющего условиям 1.4) такого закона, который дает средние (для класса симметричных одномодальных усеченных законов распределений) значения определяемых характеристик. При этом погрешности получаемых характеристик - наименьшие среди получаемых для всех других возможных видов симметричных одномодальных усеченных распределений. Эти погрешности также приведены в приложении Б.
2.9. При оформлении результатов измерений, связанных с международными работами (международные сличения эталонов, поверка или калибровка средств измерений для зарубежных стран), а также с исследованиями первичных государственных эталонов, вместо характеристик погрешности измерений может быть использована неопределенность измерений (приложение Г) в соответствии с международной рекомендацией «Guide to the expression of uncertainty in measurement». В этом случае среднее квадратическое отклонение погрешности измерений (п.2.4) эквивалентно стандартной неопределенности (standard uncertainty 2.3.1 «Guide») или суммарной стандартной неопределенности (combined standard uncertainty 2.3.4 «Guide»); границы, в которых погрешность измерений находится с заданной вероятностью (п.2.4) эквивалентны расширенной неопределенности (expanded uncertainty 2.3.5 «Guide»).
3 ФОРМЫ ПРЕДСТАВЛЕНИЯ ХАРАКТЕРИСТИК ПОГРЕШНОСТИ ИЗМЕРЕНИИ
3.1. Погрешность измерений по 2.1.1 и 2.1.2 представляют характеристиками из числа приведенных в графах 2, 3 таблицы 1 с указанием совокупности условий, для которых принятые характеристики действительны. В состав этих условий могут входить: диапазон значений измеряемой величины; частотные спектры измеряемой величины, или диапазон скоростей ее изменений, или частотные спектры, диапазоны скоростей изменений параметров, функционалом которых является измеряемая величина; диапазоны значений всех величин, существенно влияющих на погрешность измерений (средств измерений), а также при необходимости и другие факторы.
3.1.1 Характеристики погрешности измерений указывают в единицах измеряемой величины (абсолютные) или процентах (долях) от результатов измерений (относительные).
Примеры к 3.1:
Пример 1 - Запись в техническом задании на разработку МВИ расхода жидкости (норма).
Норма на абсолютную погрешность измерений расхода жидкости: Δр = ±0,2 м3/с, Р=0,95. Условия, при которых погрешность измерений должна находиться в заданных границах: диапазон значений измеряемого расхода от 10 до 50 м3/с, температура жидкости от 15 до 30°С, кинематическая вязкость жидкости от 1·10-6 до 1,5·10-6 м2/с.
Пример 2 - Запись в аттестате МВИ добротности катушки индуктивности (приписанная погрешность).
Наибольшее возможное значение среднего
квадратического отклонения случайной составляющей абсолютной погрешности
измерений ![]() = 0,08; наибольшее возможное значение
среднего квадратического отклонения неисключенной систематической составляющей
абсолютной погрешности измерений σM[Δs]= 0,1. Условия,
для которых определены характеристики погрешности измерений: диапазон значений
измеряемой добротности от 50 до 80; диапазон частот тока, протекающего через
катушку, от 50 до 300 Гц; диапазон температур среды, окружающей катушку и
применяемые средства измерений, от 15 до 25 °С; коэффициент нелинейных
искажений тока не более 1 %.
= 0,08; наибольшее возможное значение
среднего квадратического отклонения неисключенной систематической составляющей
абсолютной погрешности измерений σM[Δs]= 0,1. Условия,
для которых определены характеристики погрешности измерений: диапазон значений
измеряемой добротности от 50 до 80; диапазон частот тока, протекающего через
катушку, от 50 до 300 Гц; диапазон температур среды, окружающей катушку и
применяемые средства измерений, от 15 до 25 °С; коэффициент нелинейных
искажений тока не более 1 %.
Примечание
При практических записях характеристик погрешностей измерений необязательно каждый раз записывать словами название характеристики и условия, которым они соответствуют. Целесообразно записывать их условными обозначениями, приложив отдельный список обозначений.
При регистрации характеристик погрешности измерений с помощью автоматических устройств рекомендуется обозначать характеристики словами и не использовать условные обозначения.
3.2. Статистические оценки характеристик погрешности измерений по 2.1.3. представляют одной или при необходимости несколькими характеристиками из числа приведенных в графе 4 таблицы 1.Дополнительно могут быть указаны частотный спектр или скорость изменения измеряемой величины, или частотный спектр, скорость изменения параметров, функционалом которых является измеряемая величина; значения или диапазоны значений существенно влияющих величин, а также при необходимости и другие факторы, характеризующие проведенные измерения.
Примечание
Каждую статистическую оценку характеристики погрешности измерений относят к определенному результату измерений.
3.2.1. Статистические оценки характеристик погрешности измерений указывают в единицах измеряемой (абсолютные) или в процентах (долях) от результата измерений (относительные).
3.3. Характеристики погрешности измерений и их статистические оценки могут быть указаны в виде постоянных величин или как функции времени, измеряемой или другой величины в виде формулы, таблицы, графика.
3.4. Характеристики погрешности и их статистические оценки выражают числом, содержащим не более двух значащих цифр. При этом для статистических оценок характеристик третий разряд (неуказываемый младший) округляют в большую сторону. Допускается характеристики погрешности и их статистические оценки выражать числом, содержащим одну значащую цифру. В этом случае для статистических оценок характеристик число получают округлением в большую сторону, если цифра последующего неуказываемого младшего разряда равна или больше пяти, или в меньшую сторону, если эта цифра меньше пяти.
3.5. Характеристики погрешности измерений и условия, для которых они действительны, указывают совместно с результатом измерений, к которому их относят, или совместно с группой результатов измерений, к которым их относят, или в свидетельстве об аттестации МВИ, по которой получены данные результаты измерений.
4 ФОРМЫ ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
4.1. Результат измерений представляют именованным или неименованным числом.
Пример - 100 кВт; 20 °С - именованные числа;
0,44; 2,765 - неименованные числа.
4.2. Совместно с результатом измерений представляют характеристики его погрешности или их статистические оценки. Если результат измерений или определенная группа результатов измерений получены по аттестованной МВИ, то их можно сопровождать вместо характеристик погрешности измерений ссылкой на свидетельство об аттестации МВИ, удостоверяющее характеристики погрешности получаемых при использовании данной МВИ результатов измерений и условия ее применимости.
4.2.1. Если результат измерений получен по такой МВИ, когда характеристики погрешности измерений оценены в процессе самих измерений или непосредственно после или перед ними, результат сопровождают статистическими оценками характеристик погрешности измерений.
4.3. Допускается представление результата измерений доверительным интервалом, покрывающим с известной (указываемой) доверительной вероятностью истинное значение измеряемой величины. В этом случае статистические оценки характеристик погрешности измерений отдельно не указывают.
Примечание - Такая форма представления результатов измерений допускается в случаях, когда характеристики погрешности измерений заранее не установлены и погрешность измерений оценивают в процессе самих измерений или непосредственно после или перед ними.
4.4. Совместно с результатом измерений при необходимости приводят дополнительные к указанным в 3.1 данные.
4.4.1. Представление результатов измерений изменяющейся во времени измеряемой величины при необходимости сопровождают указаниями моментов времени, соответствующих каждому из представленных результатов измерений. При этом началом шкалы времени может служить любой момент времени, принятый для данного эксперимента в качестве начального.
4.4.2. Представление результатов измерений, полученных как среднее арифметическое значение результатов многократных наблюдений, сопровождают указанием числа наблюдений и интервала времени, в течение которого они проведены. Если измерения, при которых получены данные результаты, проводят по МВИ, установленной в каком-либо документе, вместо указания числа наблюдений и интервала, допускается ссылка на этот документ.
4.4.3 При необходимости для правильной интерпретации результатов и погрешности измерений указывают, для данной МВИ модель объекта измерений и ее параметры, принятые в качестве измеряемых величин. Если измеряемую величину выражают функционалом, последний также указывают.
4.4.4 При необходимости результат измерений и характеристики погрешности измерений сопровождают указанием соответствия (или несоответствия) характеристик погрешности нормам точности измерений, если они заданы.
Примеры к 4.4:
Пример 1 - Запись в протоколе результата измерений расхода жидкости, полученного по аттестованной МВИ:
а) Результат измерений 10,75м3/с; |Δl| |Δh | = 0,15 м3/с; Р=0,95. Условия измерений: температура жидкости 20 °С, кинематическая вязкость 1,5·10-6 м2/с;
б) Результат измерений 10,75м3/с. Характеристики погрешности и условия измерений - в соответствии со свидетельством об аттестации МВИ № 17 от 05.07.2003 г.
Пример 2 - Запись в протоколе результата измерений расхода жидкости, полученного по неаттестованной МВИ. Статистические оценки характеристик погрешности измерений определены в процессе измерений:
а) Результат измерений 10,75 м3/с; σ̃[ْΔ] = 0,08 м3/с; σ̃[Δs] = 0,10 м3/с. Условия измерений: температура жидкости 20°С, кинематическая вязкость 1,5·10-6 м2/с;
б)Значение измеряемого расхода - в интервале от 10,50 до 11,00 м3/с с доверительной вероятностью 0,95. Условия измерений: температура жидкости 20°С, кинематическая вязкость 1,5·10-6 м2/с.
Пример 3 - Запись в протоколе результатов измерений изменяющегося электрического напряжения u(t), полученных по аттестованной МВИ:
|
U(t), В |
7,55 |
3,15 |
-0,35 |
-0,50 |
-4,70 |
-1,57 |
|
t, с |
0 |
1 |
2 |
3 |
4 |
5 |
Характеристики погрешности и условия измерений - в соответствии со свидетельством об аттестации МВИ № 5 от 17.01.2003 г.
Пример 4 - Запись в протоколе результата измерений, полученного как среднее арифметическое результатов наблюдений температуры по аттестованной МВИ:
Результат измерений 263,7 °С. Число наблюдений - 50, в течение 49 мин. Характеристики погрешности и условия измерений - в соответствии со свидетельством об аттестации МВИ № 13 от 23.01.2003 г.
5 ИСПОЛЬЗОВАНИЕ РЕЗУЛЬТАТОВ И ХАРАКТЕРИСТИК ПОГРЕШНОСТИ ИЗМЕРЕНИЙ ПРИ ИСПЫТАНИЯХ И КОНТРОЛЕ ПАРАМЕТРОВ ОБРАЗЦОВ (ПРОБ) ПРОДУКЦИИ
5.1 В настоящей рекомендации рассматриваются следующие области использования измерений.
5.1.1 Определение значения отдельного параметра образца (пробы) материального объекта при заданных значениях параметров режима работы образца и параметров условий, в которых находится образец (далее - параметров условий испытаний); данную экспериментальную операцию в настоящей рекомендации называют испытаниями образца объекта (далее - образца).
5.1.2 Контроль параметра образца (пробы) на соответствие требованию, заданному в виде х1≤ х≤ хh при ξl= ξIN,...ξm = ξmN, где х - истинное значение контролируемого параметра образца;xh, и xl - верхняя и нижняя границы допускаемых значений параметра х, соответственно; ξl,..., ξm - параметры условий контроля; ξIN,…, ξmN - номинальные значения параметров условий контроля; m - количество существенно влияющих и, следовательно, учитываемых условий контроля.
Примечание - Рассматриваются только однопараметровые испытания и контроль.
5.2 За результат испытаний образца принимают результат измерений параметра, определяемого при испытаниях, при фактически установленных значениях параметров условий испытаний. Результат испытаний сопровождают указанием характеристик погрешности испытаний (или статистических оценок характеристик), а также номинальных значений параметров условий испытаний и действительных или допускаемых характеристик погрешности задания этих параметров (или статистических оценок характеристик) или ссылкой на документ, где они указаны.
5.3 За погрешность испытаний образца принимают разность между результатом измерений параметра, определяемого при испытаниях образца продукции, полученным при фактических условиях испытаний, и истинным значением определяемого параметра, которое он имеет при параметрах условий испытаний, точно равных своим номинальным значениям или тем значениям, при которых требуется определять параметр образца. Определенная таким образом погрешность испытаний характеризует степень достижения цели испытаний по 5.1.1.
5.4 Результатом контроля параметра образца (или контроля образца) является суждение о том, находится или не находится значение контролируемого параметра образца в заданных границах. Результат контроля сопровождают указанием показателей достоверности контроля, а также номинальных значений параметров условий контроля и характеристик погрешности задания этих параметров (или статистических оценок характеристик), или ссылкой на документ, где они указаны.
5.5 В качестве характеристик погрешности испытаний образцов используют характеристики, аналогичные приведенным в таблице 1 для погрешности измерений.
5.6 Математическое определение погрешности испытаний образцов продукции приведено в приложении Д.
5.7 В настоящей рекомендации рассматриваются две группы показателей достоверности контроля образцов:
5.7.1 Наибольшая вероятность ошибочного признания годным любого в действительности дефектного образца; наибольшая средняя для совокупности образцов (или наибольшая для отдельного образца) вероятность ошибочного отнесения к дефектным в действительности годных образцов; наибольшее отклонение контролируемого параметра от номинального значения у образцов, ошибочно признанных годными.
5.7.2 Вероятность неправильности суждения о годности образца, признанного по результатам контроля годным; вероятность неправильности суждения о дефектности образца, признанного по результатам контроля дефектным.
Примечание - Показатели по 5.7.1 относят к методикам измерительного контроля, предусматривающим фиксацию только результата контроля ("годен" - "не годен"), и к устройствам допускового контроля. Показатели по 5.7.2 относят к методикам измерительного контроля, предусматривающим фиксацию результата измерений контролируемого параметра образца.
5.8 Математические определения показателей достоверности измерительного контроля образцов продукции приведены в приложении Д.
5.9 Функциональные взаимосвязи показателей достоверности контроля параметра образца продукции с погрешностью измерений при контроле приведены в приложении Е.
5.10 Инженерные способы расчета характеристик погрешности испытаний образца продукции по известным характеристикам погрешности измерений параметра, определяемого при испытаниях, характеристикам функций влияния условий испытаний на определяемый параметр, характеристикам погрешностей воспроизведения номинальных условий испытаний приведены в приложении Ж.
5.11 Инженерные способы определения основных показателей достоверности методик контроля образцов продукции по известным характеристикам погрешности измерений при контроле и параметрам методик контроля приведены в приложении И.
ПРИЛОЖЕНИЕ А
Конечные цели измерений и рекомендации по выбору измеряемых величин
А.1 Измерения не являются самоцелью, а имеют определенную область использования, т.е. их проводят для достижения некоторого конечного результата. Конечный результат не обязательно представляет собой оценку истинного значения измеряемой величины. В зависимости от назначения измерений (для контроля параметров продукции, для испытаний образцов продукции с целью установления ее технического уровня, для учета материальных и энергетических ресурсов, для диагностики технического состояния машин и др.) конечный результат в том или ином виде отражает требуемую информацию о количественных свойствах явлений, процессов (в том числе, технологических), материальных объектов (материалов, полуфабрикатов, изделий и т.п.). В данном случае речь идет только о той информации, которая может быть получена путем измерений. Вследствие этого результат измерений следует рассматривать как промежуточный результат, и номенклатуру характеристик погрешности измерений выбирают, исходя из требуемого конечного результата (результат испытаний или контроля, результат оценки эффективности управления технологическим процессом и др.), методики его расчета, формы представления показателей достоверности конечного результата.
Для этого устанавливают функциональную взаимосвязь результата измерений и характеристик погрешности измерений с требуемым конечным результатом и характеристиками (показателями) его погрешности (достоверности). Например, для планирования процессов испытаний и измерительного контроля параметров продукции, проводимых путем измерений, устанавливают функциональную взаимосвязь результатов и характеристик погрешности измерений с результатами испытаний и измерительного контроля параметров образца продукции, а также с характеристиками погрешности испытаний и показателями достоверности измерительного контроля.
А.2 Для обоснованного планирования измерений и правильной интерпретации результатов и погрешности измерений на начальном этапе решения задачи измерений (например, при разработке МВИ) принимают определенную модель объекта измерений, достаточно адекватную (для решения данной технической задачи) свойствам объекта измерений. В качестве измеряемой величины выбирают такой параметр модели, который также наиболее близко соответствует данной цели измерений. Значение параметра модели, т.е. значение измеряемой величины, может быть выражено числом, функцией или функционалом. Это учитывают при разработке МВИ и при выборе средств измерений.
Пример А.1 - Объект измерений - вал. В соответствии с конечной задачей, решаемой путем измерений, и с априорной информацией о свойствах объекта в качестве модели вала принимают прямой круговой цилиндр. Параметр модели - измеряемая величина - диаметр окружности цилиндра в любом его поперечном сечении; его значение выражают числом.
Пример А.2 - Объект
измерений - поршень грузопоршневого манометра. Цель измерений - определение
эффективной площади поршня. В соответствии с априорной информацией о том, что
поперечное сечение поршня может незначительно отличаться от круга, в качестве
модели поршня принимают прямой цилиндр, поперечное сечение которого близко к
кругу. Эффективную площадь поршня в некоторых случаях определяют по среднему
диаметру его поперечного сечения. Соответственно цели измерений в качестве
параметра модели - измеряемой величины - принимают средний диаметр поперечного
сечения поршня. Значение измеряемой величины в данном случае можно выразить,
например, функционалом вида ![]() , где d(a1) - диаметр
имеющий угловую координату a1
=30(i - 1), т.е.
функция аргумента a1 в угловых градусах.
, где d(a1) - диаметр
имеющий угловую координату a1
=30(i - 1), т.е.
функция аргумента a1 в угловых градусах.
Пример А.3 - Объект измерений - изменяющееся электрическое напряжение. Цель измерений - оценка мощности, которая может быть выделена в нагрузку. В соответствии с априорной информацией о том, что форма кривой напряжения близка к синусоидальной, в качестве модели напряжения принимают синусоидальное напряжение. Соответственно цели измерений в качестве параметра модели - измеряемой величины - принимают эффективное (действующее) значение напряжения.
Значение измеряемой величины выражают функционалом![]()
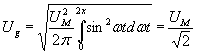 ,
,
где Um и
![]() - амплитуда
и круговая частота синусоидального напряжения. Если информация о форме кривой
напряжения отсутствует, то в качестве модели напряжения, например, может быть
принято случайно изменяющееся электрическое напряжение. Тогда значение
измеряемой величины может быть выражено функционалом
- амплитуда
и круговая частота синусоидального напряжения. Если информация о форме кривой
напряжения отсутствует, то в качестве модели напряжения, например, может быть
принято случайно изменяющееся электрическое напряжение. Тогда значение
измеряемой величины может быть выражено функционалом
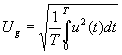 ,
,
где Т - время интегрирования;
и (t) - реализация случайного процесса - функция времени t.
ПРИЛОЖЕНИЕ Б
Методика расчета границ интервала, в котором находится погрешность
измерений с заданной вероятностью, меньшей единицы, по среднему квадратическому
отклонению погрешности измерений
Нижняя Δ1 и верхняя Δh, границы интервала, в котором погрешность измерений находится с заданной вероятностью Р, могут быть определены по формуле
где К(Р) - коэффициент, зависящий от вероятности Р;
σ - среднее квадратическое отклонение погрешности измерений.
Если границы интервала рассчитывают по нормированному среднему квадратическому отклонению, то в формулу подставляют значение предела допускаемого среднего квадратического отклонения; при этом в результате расчета по формуле получают оценку сверху границ интервала.
При соблюдении условий 1.4 коэффициент К(Р) может быть определен по графику (рисунок Б.1)
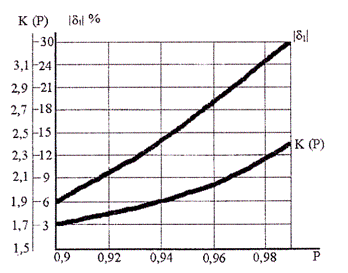
Рисунок Б.1
При этом модуль наибольшей возможной относительной погрешности |δ| коэффициента К(Р) также определяют по соответствующему графику(рисунок Б.1).
Графики дают результаты, идентичные получаемым по графику РД 50-453.
Если функция плотности распределения вероятностей погрешности измерений не удовлетворяет хотя бы одному из условий 1.4 настоящей рекомендации, то границы интервала, в котором погрешность измерений находится с заданной вероятностью Р, могут быть рассчитаны по формуле (Б.1) (предварительно определяют функцию К(Р), соответствующую действительной функции плотности).
Для приближенных расчетов границ интервала в качестве оценок сверху коэффициента К(Р) в диапазоне значений вероятности Р от 0,9 до 0,98 может быть использована формула
К(Р) = 5 (Р - 0,5). (Б.2)
ПРИЛОЖЕНИЕ В
Основные обозначения
Δ- абсолютная погрешность измерений;
δ - относительная погрешность измерений;
Δ S - абсолютная систематическая составляющая погрешности измерений;
![]() -
абсолютная случайная составляющая погрешности измерений;
-
абсолютная случайная составляющая погрешности измерений;
Р - вероятность;
σ- среднее квадратическое отклонение абсолютной погрешности измерений (ее составляющих);
х - контролируемый параметр
Δx - отклонение контролируемого параметра от номинального значения;
XN - номинальное значение параметра;
Х1, Xh - нижняя и верхняя границы допускаемых значений параметра х;
L(ΔX) - оперативная характеристика;
Рbam - наибольшая вероятность ошибочного признания (при реализации данной методики контроля) годным любого в действительности дефектного образца (для отдельного образца);
(Δхм)ba - наибольшее по абсолютному значению возможное отклонение контролируемого параметра любого образца, который при реализации данной методики контроля может быть ошибочно признан годным;
![]() - наибольшая средняя по совокупности годных
образцов вероятность ошибочного признания (при реализации данной методики
контроля) дефектным в действительности годных образцов;
- наибольшая средняя по совокупности годных
образцов вероятность ошибочного признания (при реализации данной методики
контроля) дефектным в действительности годных образцов;
![]() – средняя на совокупности всех контролируемых образцов
вероятность ошибочного признания (при реализации данной методики контроля)
дефектными в действительности годных образцов;
– средняя на совокупности всех контролируемых образцов
вероятность ошибочного признания (при реализации данной методики контроля)
дефектными в действительности годных образцов;
PgrM - наибольшая вероятность ошибочного признания (при реализации данной методики контроля) дефектным любого в действительности годного образца (для отдельного образца);
![]() -
вероятность ошибочности суждения о годности данного образца, признанного по
результатам контроля годным (при уже полученном результате контроля);
-
вероятность ошибочности суждения о годности данного образца, признанного по
результатам контроля годным (при уже полученном результате контроля);
![]() - вероятность
ошибочности суждения о дефектности данного образца, признанного по результатам
контроля дефектным (при уже полученном результате контроля);
- вероятность
ошибочности суждения о дефектности данного образца, признанного по результатам
контроля дефектным (при уже полученном результате контроля);
G - граница поля допуска для отклонения Δх.;
Gy - граница поля контрольного допуска, с которой
сравнивают оценку ![]() с целью принятия
решения о годности или дефектности образца;
с целью принятия
решения о годности или дефектности образца;
Gβ - граница такой области значений Δх, для которой отрицательные результаты контроля (образец признают дефектным) принято считать ошибочным;
Pg(![]() х)
- вероятность того, что при полученной в результате измерений (при контроле)
оценке
х)
- вероятность того, что при полученной в результате измерений (при контроле)
оценке ![]() х отклонения контролируемого параметра
образца истинное значение Δх
отклонения параметра находится в границах поля допуска;
х отклонения контролируемого параметра
образца истинное значение Δх
отклонения параметра находится в границах поля допуска;
(ΔP)21 - наибольшая возможная погрешность вероятности Рbam, обусловленная отличием реального вида функции плотности распределения вероятностей погрешности измерений от того вида функции плотности , которому соответствует график Рbam на рисунке И 1;
(ΔР)22 - то же для графика Рbam на рисунке И.2;
(ΔР)11- наибольшая возможная погрешность вероятности
(Pgr)Mg, обусловленная отличием реального вида функции плотности распределения вероятностей погрешности измерений от того вида функции плотности, которому соответствует график на рисунке И.3;
(ΔP)12 - то же для графика на рисунке И.4;
Δx - плотность распределения вероятностей отклонения Δx на совокупности контролируемых образцов;
φ(Δk) - плотность распределения вероятностей погрешности измерений при контроле.
Индексы
1 - нижняя (low),
h - верхняя (high),
g - годный (good),
b - дефектный (bad),
a - признанный годным (accepted),
г - признанный дефектным (rejected),
I - контролируемый (inspected),
ex - испытание (examination),
N - номинальное (nomina).
ПРИЛОЖЕНИЕ
Г
Неопределенность измерений
В 2.2.3 «Guide to the expression of uncertainty in measurement» (Первое издание ISO 1993, русский перевод «Руководство по выражению неопределенности измерений», С.-Петербург, ВНИИМ им. Д.И. Менделеева, 1993, далее Руководство) неопределенность измерений определена как «параметр, связанный с результатом измерения, который характеризует рассеяние значений, которые могли быть обоснованно приписаны измеряемой величине». В Руководстве рассматриваются измеряемые величины, характеризуемые единственным значением (1.2 Руководства).
Различие между погрешностью и неопределенностью измерений сводится к различию систем координат, относительно которых рассматривают истинное значение измеряемой величины и результат измерений. При рассмотрении погрешности измерений систему координат привязывают к истинному значению измеряемой величины, наблюдая рассеяние результата измерений (рисунок Г.1); при рассмотрении неопределенности измерений - к результату измерений, что и создает эффект рассеяния единственного значения измеряемой величины (рисунок Г.2)
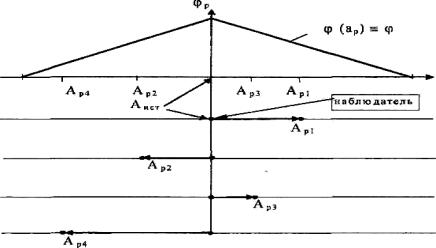
Рисунок Г. 1
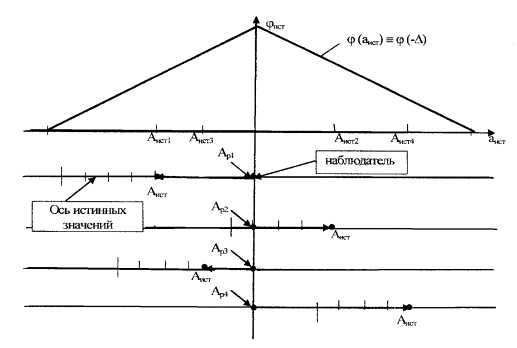
Рисунок Г.2
Обозначения на рисунках:
ар - результат измерений (Аpi- реализации результата измерений - по 1.1 настоящей рекомендации);
Аист - истинное значение измеряемой величины (Аистi - реализация истинного значения измеряемой величины в системе координат, привязанной к результату измерений);
Δ- погрешность измерений;
φ(ар) - плотность распределения вероятности результата измерений;
φ (Δ) - плотность распределения вероятностей погрешности измерений;
ф (аист) - плотность распределения вероятностей единственного истинного значения измеряемой величины, наблюдаемая в системе координат, привязанной к результату измерений.
Таким образом, неопределенность измерений в соответствии с 2.2.3 Руководства может быть определена как параметр центрированной случайной величины, представляющей собой разность между истинным значением измеряемой величины и результатом измерений, т.е. величины, совпадающей по модулю с погрешностью измерений, но противоположной ей по знаку. Закон распределения вероятностей этой случайной величины φ(-Δ) представляет собой зеркальное отражение закона распределения вероятностей погрешности измерений. Количественно характеристики погрешности измерений и соответствующие виды неопределенности измерений совпадают (п.п. Е.5.3 и Е.5.4 Руководства).
ПРИЛОЖЕНИЕ Д
Математические определения погрешности испытаний и показателей
достоверности измерительного контроля образцов продукции
Д.1 Погрешность Δех испытаний образца определяют по формуле
Δех = Δ*Δ1F'1N(ξ1)*….* Δ mF'mN(ξm), (Д.1)
где Δ- погрешность измерений параметра, определяемого при испытаниях;
Δi - погрешность воспроизведения или измерений i-гo параметра ξ1 условий испытаний;
FiN(ξi) - производная функции зависимости параметра, определяемого при испытаниях, от параметра ξi в точке ξi; = ξiN
ξiN - номинальное значение параметра ξi;
* - символ объединения (суммирования) случайных величин (процессов);
m - количество учитываемых условий испытаний.
Д.2 Наибольшую вероятность Рbam ошибочного признания (при реализации данной методики измерительного контроля) годным любого в действительности дефектного образца определяют по формуле
Рbam =L(Δx) в точке | Δx | = |G|, (Д.2)
где Δх - отклонение контролируемого параметра х образца от номинального значения хм, выраженное в единицах контролируемого параметра;
G - граница поля допуска для отклонения Δх, определяющая годность или дефектность образца продукции по контролируемому параметру;
L (Δx) - оперативная характеристика - зависимость вероятности признания годным образца при его контроле от значения Δx
Д.2.1 Отклонение Δx определяют путем вычитания номинального значения xn параметра контролируемого образца из действительного значения х параметра; нижнюю и верхнюю границы поля допуска (G1, Gh) для отклонений Δx определяют путем вычитания номинального значения xN из границ (x1,xh) поля допускаемых значений параметра. Принято: xh – xN = xN – x1, следовательно, Gh = -Gi = G.
Д.2.2 Вероятность Рbam - наибольшая из тех, которые могут иметь место при | Δx] ≥ G.
Д.2.3 Оперативная характеристика LΔx Х) отражает свойства методики контроля.
Д.3 Наибольшее по абсолютному значению возможное отклонение (Δxм)ba контролируемого параметра образца, который (при реализации данной методики измерительного контроля) может быть ошибочно признан годным, определяют по формуле
где ![]() - условная (при
условии, что Δx = (ΔхM)ba) плотность
распределения вероятностей оценки
- условная (при
условии, что Δx = (ΔхM)ba) плотность
распределения вероятностей оценки ![]() отклонения Δх получаемой путем измерений при измерительном
контроле;
отклонения Δх получаемой путем измерений при измерительном
контроле;
Gr - граница поля контрольного допуска, с которой
сравнивают оценку ![]() с целью принятия
решения о годности или дефектности образца (|Gγ|≤G).
с целью принятия
решения о годности или дефектности образца (|Gγ|≤G).
Д.4 Наибольшая средняя для
совокупности годных образцов вероятность ![]() ошибочного признания (при реализации
данной методики измерительного контроля) дефектными в действительности годных
образцов определяют по формуле
ошибочного признания (при реализации
данной методики измерительного контроля) дефектными в действительности годных
образцов определяют по формуле
где Gβ - граница такой области (0≤| Δx|≤|Gβ|) значений | Δх|, для которой отрицательные результаты измерительного контроля (образец признают дефектным) рекомендуется считать ошибочными (|Gβ |≤|G).
Д.4.1 Вероятность ![]() характеризует долю
неверно забракованных в области с границами Gβ образцов (Ngr) в общем количестве (Ng) годных образцов:
характеризует долю
неверно забракованных в области с границами Gβ образцов (Ngr) в общем количестве (Ng) годных образцов:
![]() (Д.4а)
(Д.4а)
Д.4.2 Формула (Д.4)
справедлива при равномерном законе распределения вероятностей отклонений Δх по совокупности
годных образцов и может быть использована для расчетов ![]() - в тех случаях, когда закон распределения
вероятностей отклонений по всем контролируемым образцам неизвестен. В случаях,
когда закон распределения вероятностей отклонений Δх по всем контролируемым образцам задан
(известен), более предпочтительным (по сравнению с
- в тех случаях, когда закон распределения
вероятностей отклонений по всем контролируемым образцам неизвестен. В случаях,
когда закон распределения вероятностей отклонений Δх по всем контролируемым образцам задан
(известен), более предпочтительным (по сравнению с ![]() ) показателем достоверности контроля является средняя по
совокупности всех контролируемых образцов вероятность (Pgr)
ошибочного признания дефектными в действительности годных образцов,
определяемая формулой
) показателем достоверности контроля является средняя по
совокупности всех контролируемых образцов вероятность (Pgr)
ошибочного признания дефектными в действительности годных образцов,
определяемая формулой
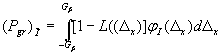 (Д.5)
(Д.5)
где φI(Δх) - плотность распределения вероятностей отклонений Δх по совокупности контролируемых образцов.
Д.4.3 Вероятность ![]() характеризует долю
неверно забракованных в области с границами ±Gβ
образцов в общем количестве (NI)
контролируемых образцов:
характеризует долю
неверно забракованных в области с границами ±Gβ
образцов в общем количестве (NI)
контролируемых образцов:
![]() (Д.5а)
(Д.5а)
Д.4.4 Выделение области (0< | Δх | ≤ | Gβ |), т.е. введение в расчеты границы |Gβ | < G имеет смысл в тех случаях, когда контролируемый параметр образца может после контроля измениться настолько, что вскоре после осуществления контроля возможен его выход за границы поля допуска. Ведение | Gβ | < G учитывает заинтересованность заказчика в признании дефектными таких образцов, параметры которых, хотя и находятся в границах поля допуска, но близки к этим границам, и, следовательно, образцы вскоре могут потребовать ремонта. Если границу Gβ не вводят, то в формуле (Д.4) принимают | Gβ | = G и формула (Д.4) принимает вид
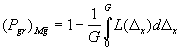 (Д.6)
(Д.6)
Д.4.5 Для отдельного образца наибольшую вероятность ошибочного признания (при реализации данной методики измерительного контроля) дефектным любого в действительности годного образца определяют по формуле
PgrM = 1-L(Δх) (Д.7)
при | Δх | = |Gp|, если вводится граница Gβ
| Δх| = G, если граница Gβ не вводится
и считают наибольшей из тех, которые могут иметь место при | Δх| ≤ |Gβ| или | Δх |≤G.
Д.5 Вероятность ![]() неправильности
суждения о годности данного образца, признанного по результатам измерительного
контроля годным, определяют по формуле
неправильности
суждения о годности данного образца, признанного по результатам измерительного
контроля годным, определяют по формуле
![]() при |
при |![]() | ≥ |Gγ| (Д.8)
| ≥ |Gγ| (Д.8)
а вероятность ![]() неправильности
суждения о дефектности данного образца, признанного по результатам
измерительного контроля дефектным, - по формуле
неправильности
суждения о дефектности данного образца, признанного по результатам
измерительного контроля дефектным, - по формуле
![]() при |
при |![]() | ≤ |Gγ|, (Д.9)
| ≤ |Gγ|, (Д.9)
где ![]() - вероятность
того, что при полученной в результате измерений (при контроле) оценке
- вероятность
того, что при полученной в результате измерений (при контроле) оценке ![]() отклонения контролируемого параметра
образца истинное значение Δx отклонения параметра
находится в границах поля допуска, т.е. |Δx|≤G. Характеристика
отклонения контролируемого параметра
образца истинное значение Δx отклонения параметра
находится в границах поля допуска, т.е. |Δx|≤G. Характеристика ![]() отражает
свойства методики измерительного контроля. Вероятности
отражает
свойства методики измерительного контроля. Вероятности ![]() и
и ![]() Ръ могут быть использованы при оценке правильности
уже полученного результата контроля параметра образца продукции.
Ръ могут быть использованы при оценке правильности
уже полученного результата контроля параметра образца продукции.
ПРИЛОЖЕНИЕ Е
Функциональные связи показателей достоверности контроля параметра
образца продукции с погрешностью измерений при контроле
Е.1 Функциональная связь наибольшей вероятности Рbam ошибочного признания (при реализации данной методики контроля) годным любого в действительности дефектного образца (по Д.2) с погрешностью измерений при контроле определяется формулой
![]()
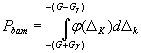 для точки Δх = G (Е.1)
для точки Δх = G (Е.1)
или
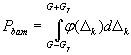 для точки Δх =-G, (Е1а)
для точки Δх =-G, (Е1а)
где φ(Δk) - плотность распределения вероятностей погрешности измерений при контроле.
Е.2.Функциональная связь наибольшего возможного отклонения (ΔхM)ba контролируемого параметра образца, который (при реализации данной методики измерительного контроля) может быть ошибочно признан годным, с погрешностью измерений при контроле (по Д.3) определяется формулой
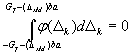 (Е.2)
(Е.2)
Е.3 Функциональная связь
наибольшей средней для совокупности годных образцов вероятности ![]() ошибочного
признания (при реализации данной методики измерительного контроля) дефектными в
действительности годных образцов (по Д.4) с
погрешностью измерений при контроле определяется формулой
ошибочного
признания (при реализации данной методики измерительного контроля) дефектными в
действительности годных образцов (по Д.4) с
погрешностью измерений при контроле определяется формулой
Если известен закон распределения вероятностей отклонений ΔхM контролируемого параметра образца по всей совокупности контролируемых образцов, то целесообразно усреднить вероятность ошибочного признания дефектными в действительности годных образцов не по совокупности годных образцов, а по совокупности всех контролируемых образцов. Связь такой средней вероятности с погрешностью измерений при контроле определяется формулой
![]()
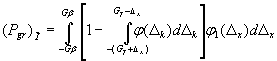 , Е.4
, Е.4
Если область (0≤|Δх|≤|Gβ|) не выделяют и границу Gβ не вводят, то в формулах (Е.3) и (Е.4) Gβ заменяют на G. При этом (Е.3) принимает вид
Связь наибольшей вероятности ошибочного признания (при реализации данной методики измерительного контроля) дефектным любого отдельного в действительности годного образца с погрешностью измерений при контроле определяют формулой
Е.4 Функциональную связь вероятности ![]() ошибочности суждения о годности данного образца, признанного
по результатам измерительного контроля годным (при известной оценке
ошибочности суждения о годности данного образца, признанного
по результатам измерительного контроля годным (при известной оценке ![]() отклонения
контролируемого параметра) (по Д.5), с
погрешностью измерений при контроле определяется формулой
отклонения
контролируемого параметра) (по Д.5), с
погрешностью измерений при контроле определяется формулой
Связь вероятности ![]() ошибочности суждения о дефектности данного образца,
признанного по результатам измерительного контроля дефектным (при известной
оценке
ошибочности суждения о дефектности данного образца,
признанного по результатам измерительного контроля дефектным (при известной
оценке ![]() отклонения
контролируемого параметра), с погрешностью измерений при контроле определяется
формулой
отклонения
контролируемого параметра), с погрешностью измерений при контроле определяется
формулой
Е.5 В случаях, когда контроль проводят при одностороннем ограничении контролируемого параметра образца (xh- верхняя граница допускаемых значений параметра х; xl - нижняя граница значения параметра х) связь показателей достоверности контроля с погрешностью измерений определяется следующими формулами:
Е.5.1 Наибольшая вероятность PbaM ошибочного признания (при реализации данной методики измерительного контроля) годным любого в действительности дефектного образца:
а) при заданной области годности образцов х ≤ xh:
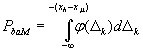 , (Е.9)
, (Е.9)
б) при заданной области годности образцов х ≥ хl:
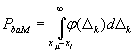 , (Е.10)
, (Е.10)
где хγh ≤ хh; хуl ≥ xl- заданные границы
результатов ![]() измерений параметра х
при контроле, при которых образец признают годным: для а) образец признают
годным, если
измерений параметра х
при контроле, при которых образец признают годным: для а) образец признают
годным, если ![]() ≤ xγh; для б) образец признают годным, если
≤ xγh; для б) образец признают годным, если ![]() ≥ хγ.
≥ хγ.
Е.5.2 Наибольшее (хmax)ba или наименьшее (хmin)ba значения контролируемого параметра образца, который (при реализации данной методики измерительного контроля) может быть ошибочно признан годным:
а) при заданной области годности образцов х ≤ хh:
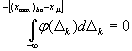 . (Е.11)
. (Е.11)
б) при заданной области годности образцов х ≥ хl:
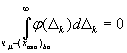 (Е.12)
(Е.12)
Е.5.3 Средняя для совокупности
контролируемых образцов вероятность ![]() ошибочного признания (при
реализации данной методики измерительного контроля) дефектными в
действительности годных образцов:
ошибочного признания (при
реализации данной методики измерительного контроля) дефектными в
действительности годных образцов:
а) при заданной области годности образцов х ≤ хh:
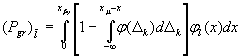 / (Е.13)
/ (Е.13)
б) при заданной области годности образцов х ≥ xl:
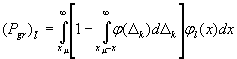
Здесь xβh ≤ xh; xβl ≥ xl - заданные границы областей таких значений параметров контролируемых образцов, для которых отрицательные результаты контроля (образец признают дефектным) принято считать ошибочными: для а) отрицательный результат контроля признают ошибочным, если х < хbh; для б) отрицательный результат контроля признают ошибочным, если х > xβl
Е.6 В случае не измерительного, а допускового контроля, когда при контроле не проводят измерений контролируемого параметра, т.е. результат и погрешность измерений контролируемого параметра отсутствуют, показатели достоверности контроля, характеризующие устройства допускового контроля, определяют приведенными выше формулами при замене в них погрешности Δk измерений при контроле на эквивалентную погрешность Δeq устройства допускового контроля, определяемую формулой
Δeq=Δγ * Δс, (Е.15)
где Δγ - погрешность задания (индикации) границ поля контрольного допуска Gγ (или, если контрольный допуск не вводят, то границ допускаG) на отклонение контролируемого параметра;
Δc - погрешность сравнения контролируемого параметра (или его отклонения) с границами поля контрольного допуска (или допуска G).
Е.7 Для определения показателей достоверности уже
полученного результата допускового контроля применяют формулы (Е.7) и (Е.8). При подстановке в них
![]() и Δeq
вместо Δk
результаты расчета представляют собой наибольшие возможные вероятности
ошибочности отдельного полученного результата допускового контроля.
и Δeq
вместо Δk
результаты расчета представляют собой наибольшие возможные вероятности
ошибочности отдельного полученного результата допускового контроля.
Е.8 Формулы, определяющие связь других показателей достоверности контроля при одностороннем ограничении контролируемого параметра с погрешностью измерений, могут быть получены аналогично формулам (Е.3) - (Е.8) с учетом при необходимости условия по Е.6.
ПРИЛОЖЕНИЕ Ж
Инженерные способы расчета характеристик погрешности испытаний образца
продукции по известным характеристикам погрешности измерений параметра,
определяемого при испытаниях, характеристикам функций влияния условий испытаний
на определяемый параметр, характеристикам погрешности воспроизведения
номинальных условий испытаний
Ж.1 К определяемым характеристикам погрешности испытаний (по 5.1.1 настоящей рекомендации) отнесены:
наибольшее по абсолютной величине возможное значение Δexm, равное половине интервала, в котором погрешность испытаний находится с вероятностью, равной единице;
наибольшее возможное среднее квадратическое отклонение σexM погрешности испытаний.
Ж.2 В соответствии с определением погрешности испытаний по Д.1 для расчета характеристик погрешности испытания могут быть применены следующие формулы:
Ж.2.1 Если в качестве исходных данных известны:
предел Δp допускаемой погрешности измерений параметра, определяемого при испытаниях;
пределы Δip допускаемой погрешности воспроизведения условий испытаний;
линейные аппроксимации (Δx/Δξi)ξi=ξiN функций влияния условий испытаний на параметр, определяемый при испытаниях, в точках номинальных значений условий испытаний,
то наибольшее по абсолютной величине возможное значение погрешности испытаний равно
![]() (Ж.1)
(Ж.1)
где m - число учитываемых условий испытаний;
Δξi - малое отклонение 1-го условия ξi испытания от номинального значения ξiN
Δх - малое изменение параметрах, определяемого при испытаниях, вызванное отклонением Δξi.
Ж.2.2 Если в качестве исходных данных известны: предел допускаемого среднего квадратического отклонения σp[Δ]погрешности измерений параметра, определяемого при испытаниях;
наибольшие возможные средние квадратические отклонения σiM (или пределы допускаемых средних квадратических отклонений σip) погрешности воспроизведения условий испытаний;
линейные аппроксимации (Δx/Δξi)ξi=ξiN функций вляния условий испытаний на параметр, определяемый при испытании, в точках номинальных значений условий испытаний,
то квадрат среднего квадратического отклонения погрешности испытаний равен
![]() (Ж.2)
(Ж.2)
Примечание - Если погрешность испытаний, определение которой дано в Д.1, удовлетворяет условиям 1.4 настоящей рекомендации, то границы интервала, в котором погрешность испытаний находится с любой вероятностью, меньшей единицы, могут быть рассчитаны по известному σexM в соответствии с приложением Б.
ПРИЛОЖЕНИЕ И
Инженерные способы определения основных показателей достоверности
методик контроля образцов продукции по известным характеристикам погрешности
измерений при контроле и параметрам методик контроля
И.1 Инженерные способы, рассматриваемые в данном приложении, применимы при соблюдении условий по 1.4 настоящей рекомендации.
И.2 К основным показателям достоверности контроля (по 5.7.1 настоящей рекомендации) образцов продукции отнесены:
И.2.1 Наибольшая вероятность РbaM ошибочного признания (при реализации данной методики контроля) годным любого в действительности дефектного образца (по Е.1).
И.2.2 Наибольшее по абсолютному значению возможное отклонение (ΔxM)ba контролируемого параметра любого образца продукции, который (при реализации данной методики контроля) может быть ошибочно признан годным (по Е.2).
И.2.3 Наибольшая средняя для совокупности годных образцов
вероятность ![]() ошибочного признания
(при реализации данной методики контроля) дефектными в действительности годных
образцов (по Е.3).
ошибочного признания
(при реализации данной методики контроля) дефектными в действительности годных
образцов (по Е.3).
И.3 К параметрам методик контроля образцов продукции отнесены:
И.3.1 Граница G поля допуска для отклонения Δx контролируемого параметра х от номинального значения хN.
И.3.2 Граница Gγ поля контрольного допуска для отклонения Δx.
И.3.3 Граница Gγ такой области отклонений Δx, для которой отрицательные результаты контроля (образец признают дефектным) принято считать ошибочными.
Примечание - Взаимосвязь параметров методик контроля с показателями достоверности контроля определена в Д.3 и Д.4.
И.4 В качестве известных характеристик погрешности измерений принимают:
а) среднее квадратическое отклонение (его наибольшее возможное значение σM[Δ] или предел допускаемого значения σp[Δ]),
б)интервал, в котором с вероятностью, равной единице, находится погрешность измерений, или пределы допускаемых погрешностей измерений ± Δр.
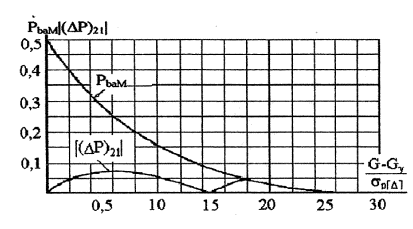
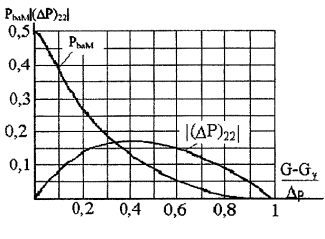
И.5 Наибольшую вероятность РbaM ошибочного признания (при реализации данной методики контроля) годным любого в действительности дефектного образца определяют с помощью графика (рисунок И.1 или рисунок И.2 в зависимости от того, какая характеристика погрешности измерений задана σр[Δ] или Δp).
И.6 Наибольшую возможную погрешность вероятности РbaM обусловленную тем, что вид реальной функции плотности распределения вероятностей погрешности измерений неизвестен, определяют по графику |( ΔР)21| (рисунок И.1) или графику |( ΔР)22| (рисунок И.2).
И.7 Наибольшее по абсолютному значению возможное отклонение (ΔxM)ba контролируемого параметра любого образца, который (при реализации данной методики контроля) может быть ошибочно признан годным, определяют по формуле
или
в зависимости от того, какая характеристика погрешности измерений задана (σp[Δ] или Δр).
Принимают К=3,5; тогда формула (И.1) дает при принятых условиях наибольшее возможное значение данного показателя.
Примечание - Если предполагают, что функция плотности распределения вероятностей погрешности измерений при контроле не только удовлетворяет условиям по 1.4 настоящей рекомендации, но отнесена к достаточно «тупым» функциям, лежащим в области между функцией плотности равномерного распределения и косинусоидальной функцией плотности распределения, то принимают К=2,5.
Рисунок И.1
Рисунок И.2
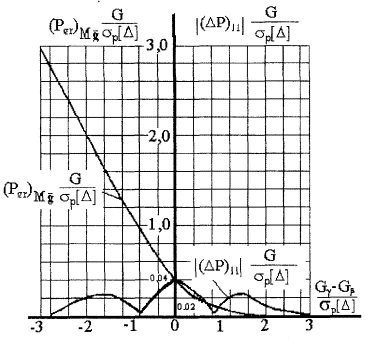
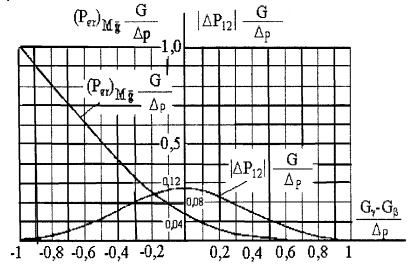
И.8 Наибольшую среднюю для совокупности годных
образцов вероятность ![]() ошибочного признания
(при реализации данной методики контроля) дефектными в действительности годных
образцов определяют графо-аналитическим способом с помощью графика
ошибочного признания
(при реализации данной методики контроля) дефектными в действительности годных
образцов определяют графо-аналитическим способом с помощью графика ![]() (рисунок И.3) или графика
(рисунок И.3) или графика ![]() (рисунок И.4) в зависимости от того, какая
характеристика погрешности измерений задана (σp[Δ] или Δp).
(рисунок И.4) в зависимости от того, какая
характеристика погрешности измерений задана (σp[Δ] или Δp).
Рисунок И.3
Рисунок И.4
Наибольшую возможную погрешность вероятности ![]() обусловленную тем,
что вид реальной функции плотности распределения вероятностей погрешности
измерений неизвестен, определяют графо-аналитическим способом по графику |(ΔP)11|G/σp[Δ] (рисунок И.3) или по графику |(ΔР)12|G/Δр | (рисунок
И.4).
обусловленную тем,
что вид реальной функции плотности распределения вероятностей погрешности
измерений неизвестен, определяют графо-аналитическим способом по графику |(ΔP)11|G/σp[Δ] (рисунок И.3) или по графику |(ΔР)12|G/Δр | (рисунок
И.4).
И.10 Данные инженерные способы могут быть применены при допусковом контроле (результаты измерений и погрешности измерений отсутствуют). При этом, вместо характеристик погрешности измерений используют соответствующую характеристику величины Δeq (по Е.6), которую предварительно рассчитывают по техническим характеристикам средства контроля.
И.11 Показатели достоверности контроля образцов продукции, приведенные в приложении Е (кроме рассмотренных в данном приложении) могут быть определены по формулам приложения Е при известной функции (или принятой аппроксимации) плотности распределения вероятностей погрешности измерений при контроле (или величины Δeq) и известных параметрах методики контроля. Также поступают, если погрешности определения показателей достоверности методик контроля образцов продукции по данному приложению для каких-либо случаев недопустимо велики.
И.12 Используя графики и формулы данного приложения,
возможно подбирать необходимые параметры методик контроля и метрологические
характеристики средств измерений и МВИ для контроля образцов продукции, а также
необходимые параметры методик и технические характеристики средств допускового
контроля образцов продукция по заданным наибольшим допускаемым показателям ![]() ,
,![]() ,
, ![]() если соблюдены
условия по 1.4 настоящей рекомендации.
если соблюдены
условия по 1.4 настоящей рекомендации.
Пример 1 - Заданы следующие параметры методики измерительного контроля и характеристики погрешности измерений: Gγ = 0,8 G; Gβ = 0,9 Gг; σр[Δ] = 0,15 G. Требуется определить:
а) наибольшую вероятность РbaM ошибочного признания (при реализации данной методики контроля) годным любого в действительности дефектного образца;
б) наибольшее по абсолютному значению возможное отклонение контролируемого параметра любого образца, который (при реализации данной методики контроля) может быть ошибочно признан годным (ΔxM)ba;
в) наибольшую
среднюю для совокупности годных образцов вероятность ошибочного признания (при
реализации данной методики контроля) дефектными в действительности годных
образцов ![]() .
.
Решение
Вероятность РbaM и погрешность ее определения находят по графикам (рисунок И.1). Параметр (G-Gγ)/σр[Δ]) равен 1,33. По графику РbaM находят, что приближенно РbaM.≈1,33 Для того же значения аргумента по другому графику находят, что погрешность (ΔР)21 определения данной вероятности приближенно находится в интервале ± 0,02. Следовательно, 0,08 ≤ РbaM ≤ 0,12.
По формуле (И.1) находят (ΔxM)ba = 0,8G + 3,5 х 0,15 G =1,3 G.
Вероятность ![]() и погрешность ее
определения находят по графикам (рисунок
И.3). Параметр (Gγ-Gβ)/σр[Δ])
равен минус 0,67. По графику
и погрешность ее
определения находят по графикам (рисунок
И.3). Параметр (Gγ-Gβ)/σр[Δ])
равен минус 0,67. По графику ![]() находят, что
приближенно эта величина равна 0,9.
находят, что
приближенно эта величина равна 0,9.
Тогда ![]() = 0,14. Для того же значения аргумента по другому
графику на том же рисунке находят, что приближенно величина [(ΔP)11Gγ/σр[Δ])
равна 0,01. Тогда погрешность, обусловленная отличием реальной функции
плотности распределения от принятой средней, лежит в пределах (ΔP)11 =
± 0,002, т.е. считают пренебрежимо мала.
= 0,14. Для того же значения аргумента по другому
графику на том же рисунке находят, что приближенно величина [(ΔP)11Gγ/σр[Δ])
равна 0,01. Тогда погрешность, обусловленная отличием реальной функции
плотности распределения от принятой средней, лежит в пределах (ΔP)11 =
± 0,002, т.е. считают пренебрежимо мала.
Пример 2 - Заданы следующие параметры методики измерительного контроля и характеристики погрешности измерений: Gγ=0,8G; Gβ=0,9G; Δp= 0,5G. Требуется определить те же показатели достоверности контроля, что и в примере 1.
Решение
Вероятность РbaM и погрешность ее определения находят по рисунку И.2. Параметр ((G - Gγ)/Δр) равен 0,4. По графику РbaM приближенно находят РbaM = 0,13. Для того же значения аргумента по другому графику на том же рисунке находят, что погрешность (ΔР)22 определения данной вероятности находится в интервале от - 0,13 до + 0,17 (так как вероятность отрицательной быть не может). Следовательно, 0≤ РbaM ≤ 0,3.
По формуле (И.2) находят (ΔxM)ba = 0,8 G + 0,5 G =1,3 G.
Вероятность ![]() - и
погрешность ее определения находят на основании графиков (рисунок И.4). Параметр (Gγ-Gβ)Δp) равен минус 0,2.
По графику
- и
погрешность ее определения находят на основании графиков (рисунок И.4). Параметр (Gγ-Gβ)Δp) равен минус 0,2.
По графику ![]() G/Δp находят, что
приближенно эта величина равна 0,26. Тогда
G/Δp находят, что
приближенно эта величина равна 0,26. Тогда ![]() =0,13. Для
того же значения аргумента по другому графику на том же рисунке находят, что
приближенно величина |(ΔР)12|G/Δp равна 0,1.
=0,13. Для
того же значения аргумента по другому графику на том же рисунке находят, что
приближенно величина |(ΔР)12|G/Δp равна 0,1.
Тогда
погрешность определения ![]() находится в интервале
± 0,05, а сама вероятность лежит в интервале 0,08≤
находится в интервале
± 0,05, а сама вероятность лежит в интервале 0,08≤![]() ≤ 0,18.
≤ 0,18.
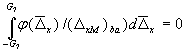
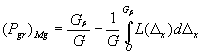
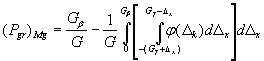
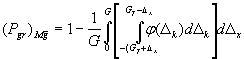 .
.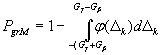 .
.